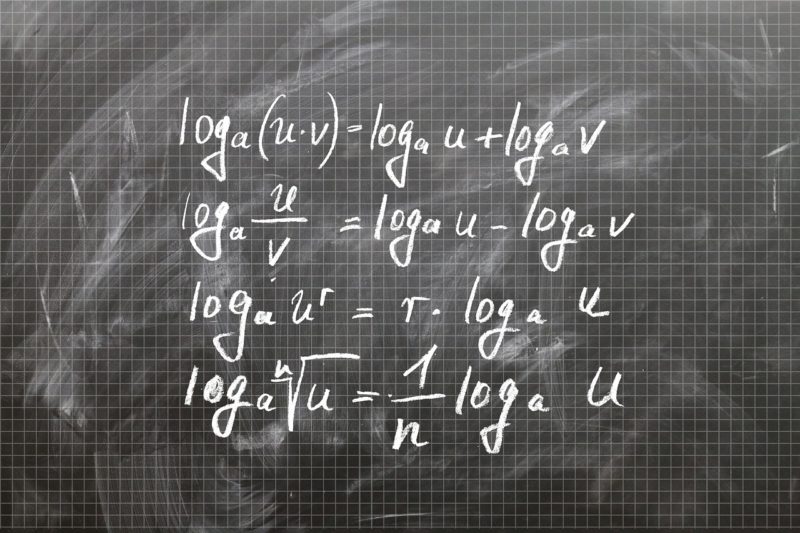A hatványfogalom fejlődése, a logaritmus kialakulása

Hatványfogalom

Bevezetése a matematika oktatásban

A hatványfogalom kialakítása már általános iskolában elkezdődik, majd középiskolában újra visszatérünk ré és tovább bővítjük. Kilencedik osztályban ismerkedünk meg a pozitív egész, a 0 és a negatív egész kitevőjű hatvány fogalmával. Tizenegyedik osztályban a hatványozást kiterjesztetjük racionális kitevőre és érzékeltetjük, hogyan lehet irracionális kitevő esetén értelmezni. A hatványfogalomnak ez az általánosítása a matematika története során nagyon hosszú, közel kétezer éves folyamat volt.

Kialakulása a matematika történetében

Jelölésrendszer az ókori görögöknél

A hatványfogalom kialakulása a pozitív egész kitevőjű hatvány fogalmával kezdődött az ókori görögöknél, többek között a III. században Alexandriában élt matematikus, Diophantosz munkáiban. Az ő jelölésrendszere a szavak rövidítésén alapult, ami átmenet volt az algebrai összefüggések szóbeli kifejezése („retorikus” algebra) és e kifejezések rövidítése („szinkopikus” algebra) között.

Diophantosz ezzel a szimbolikával az Aritmetika című művének 2-6. könyvében sok –többségükben másodfokú egyenletre vezető- problémát oldott meg. Tehát ő tekinthető a szinkopikus algebra előfutárának.

Jelölésrendszer a XVI.-XVII. századtól, Cardano

A szimbolikus algebra legnagyobb előretörése a XVI-XVII. századra tehető. E folyamatban első lépésként itt is -a Diophantosz által már használt- szinkopikus algebra jelent meg, és ezután kerültek bevezetésre második lépésként a szimbólumok. Már Cardanónál is igen jelentős ez az átmenet.

Például a

„cubus p 6 rebus aequalis 20”

azaz az

x^3+6x=20

egyenlet megoldását az alábbi alakban adta meg

 „R_xucu 108 p 10 | m R_x ucu R_x 108 m 10”

ami annyit jelent, hogy

\sqrt[3]{\sqrt{108}+10}-\sqrt[3]{\sqrt{108}-10}.

 Itt R_x (radix) természetesen a négyzetgyököt, míg az R_x ucu= radix universalis cubica a köbgyököt jelenti.

Viète jelölésrendszere

Ebben az időszakban egyre növekedett az igény arra, hogy minél egyszerűbb és tökéletesebb szimbolikát alkalmazzanak. A következetesen végigvitt egységes szimbólumrendszert minden jel szerint Viète dolgozta ki. Minden mennyiséget betűkkel jelölt, az ismeretleneket magánhangzókkal, az ismerteket mássalhangzókkal. A második és a harmadik hatvány értelmezése nála még szorosan kötődött a terület és a térfogat fogalmához. A magasabb hatványokat az előzőekre vezette vissza, például a negyedik hatványt terület-területnek, az ötödiket terület-térfogatnak, a hatodikat térfogat-térfogatnak nevezte. Tehát Viète szimbolikáját a geometriai szemlélet terheli, nem mindig érthető, váltakozva szerepelnek benne rövidített és nem rövidített szavak.

Például

„A cubus+B planum in A₃ aequatur D solido”,

ami

x^3+3Bx=D,

hisz manapság x-szel szokás jelölni az ismeretlent.

Descartes és a hatvány

Descartes volt az, aki bevezette az

a^2, {  } a^3, ...

jelölés használatát és a második, illetve harmadik hatványt függetlenítette a területtől és a térfogattól.

A racinális kitevőjűh hatvány

Az előzőekben felvázoltuk azt az utat, ami a pozitív egész kitevőjű hatványok esetén elvezetett a mai szimbólumrendszer kialakulásához. De most ugorjunk vissza 300 évet az időben. A párizsi egyetem professzora Nicolaus Oresmicus (1328-1382) volt az, aki a hatványfogalmat általánosította az által, hogy bevezette a törtkitevőjű hatványt, megadta a velük végzett műveletek szabályait és kidolgozott rájuk egy szimbolikát. Ezzel már ténylegesen megelőzi a logaritmus gondolatát. Az ő jelölésrendszerében például

\frac{1\cdot p}{2\cdot27}=27^{\frac{1}{2}}

vagy

\frac{4\cdot p}{5\cdot32}=32^{\frac{4}{5}}.

A XV. század végén a párizsi egyetemen dolgozó Nicoalus Chuquet (olv. Süké) vezette be a 0 és a negatív egész kitevőjű hatványokat. Ezeknek a fogalmaknak a pontos értelmezése és használata azonban csak a XVII. században terjedt el többek között John Wallisnek (1616-1703) köszönhetően. Ezzel egy fontos előrelépés történt a hatványfogalom fejlődésében.

Irracionális kitevőjű hatvány

Az irracionális kitevőjű hatvány precíz és pontos fogalmához szükség volt a mai igényeknek megfelelő számfogalom kialakulásához. Erre R. Dedekind (1831-1916) és G. Cantor (1845-1918) munkásságának köszönhetően a XIX. század végén, a XX. század elején került sor. Ezzel teljessé vált a hatványfogalom.

A logaritmus kialakulás

Az elméleti alapok

A logaritmust a XVII. században fedezték fel. Elméleti alapjai azonban jóval korábbra nyúlnak vissza. Az egész alapjául szolgáló gondolat, nevezetesen a számtani és mértani sorozat összehasonlításának gondolata, már az ókorban is megjelent Archimédész, ill. Diophantosz munkáiban. Később találkozunk ezzel a XIV. században Orasmicusnál, ill. a XVI. században Stifelnél a hatványfogalom általánosítása kapcsán. Ahhoz, hogy ezen a gondolat alapján a műveleteket egyszerűbb műveletekre vezessék vissza, arra volt szükség, hogy olyan táblázatok készüljenek, melyek az egymás utáni hatványokat az egymás utáni kitevőkhöz rendelik hozzá.

Az első logaritmus táblázatok

Ilyen táblázatok a XVII. század elején már léteztek, ezeket S. Stevin (1548-1620) állította össze. Az ő táblázatai nyomán készítette el az első logaritmustáblázatot J. Bürgi (1552-1632) svájci órásmester. Bürgi a prágai csillagászati obszervatóriumban dolgozott Johannes Kepler munkatársaként. A csillagászati számítások megkönnyítése érdekében alkotta meg 8 év alatt (1603-1611) logaritmustáblázatát. Sokáig nem publikálta eredményeit, csak 1620-ban adta ki könyvét Kepler sürgetésére. Késlekedése az elsőségébe került, mivel 1614-ben John Napier (1530-1617) skót báró, aki csak műkedvelőként foglalkozott tudományokkal, megjelentette A csodálatos logaritmus táblázat leírása című művét.

Táblázata elkészítésének elve, amely 1594-ben merült fel benne, ebben a korban új volt. Az érdekessége, hogy egy egyenletes és egy egyenletesen lassuló mozgást hasonlított össze, melyek kezdősebessége azonos. Az általa létrehozott logaritmus táblázat alapszáma 1/e volt, ez kissé nehézkessé tette használatát. Ezek a nehézségek vezették Napiert a tízes alapú logaritmus gondolatához, mely ebben az időben felmerült egy londoni professzor Henri Briggs (1561-1630) elméjében is. Briggs két ízben is meglátogatta Napiert Skóciában, melynek nyomán összebarátkoztak és közösen dolgozták ki az új, gyakorlatilag kényelmesebb tízes alapú logaritmusrendszert. Ennek alapja a

sorozatok összehasonlítása volt. Briggs már 1617-ben publikálta 1-től 10⁸ -ig terjedő számok 8 jegyű logaritmustáblázatát, majd 1624-ben megjelentette Logaritmikus aritmetika című részletesebb munkáját. Innentől kezdve a logaritmus a számítási technikák fontos részévé vált és az egész világon elterjedt. A XIX. században megjelentek olyan eszközök, melyek segítséget nyújtottak a gyors számításokhoz. Ilyen volt az 1827-ben elkészült logarléc is. Manapság a számítógépek világában, ezek már jelentőségüket vesztették.

(Forrás: K. A. Ribnyikov: A matematika története)

Összefoglalás

A fenti cikkben végigmentünk a hatványfogalom fejlődésén az ókori görögöktől indulva egészen a XIX. századig. Ezután kitértünk a logaritmus fogalmának kialakulására és az első logaritmustáblázatokra.

Szeretnél még több, hasonló cikket olvasni? Akkor böngéssz a blogunkon Matekos blog!

Emelt szintű érettségire készülsz, vagy elsőéves egyetemista vagy? Ekkor ajánljuk figyelmedbe az online tanuló felületünket és a felkészülést segítő csomagjainkat. Az ezekkel kapcsolatos részletekről itt ÉrettségiPro+ olvashatsz.

Összegyűjtöttük az eddigi összes emelt szintű matematika érettségi feladatsort és a megoldásokat. Ezt a gyűjteményt, valamint az érettségire készüléssel kapcsolatos hasznos tanácsokat a Emelt szintű matematika feladatsorok linken érheted el.

Szerző: Ábrahám Gábor (szakmai önéletrajz)

Cikkek

A szerző további cikkei megtalálhatók a Budapesti Fazekas Milyály Gyakorló Általános Iskola és Gimnázium matematika oktatási portálján:

• Feladatok megoldása az analízis eszközeivel.
• Függvény és inverze egyenletekben
• A háromszög területe
• Polinomalgebrai feladatok
• Szélsőértékfeladatok megoldása elemi úton

Az emelt szintű érettségire készüléssel kapcsolatos írásaink a 34 hét alatt új tudás születik, illetve 17 fejezet matematikából linken érhetők el.

A szerző által írt tankönyvek a Maxim Kiadó linken találhatók.

Matek versenyre készülőknek

Ha olyan ambícióid vannak, hogy szeretnél matematikával versenyzés szintjén foglalkozni, akkor javaslom az Erdős Pál Matematikai Tehetségondozó Iskolát. Ezzel vonatkozó részletek ezen linken Erdős Pál Matematikai Tehetséggondozó Iskola olvashatók. A matematika versenyek témáit feldolgozó könyvek, kiadványok (a szerző Egyenlőtlenségek I.-II. című könyvei is) a MATE alapítvány, kiadványok linken kersztül vásárolhatók meg.