A deltoiddal kapcsolatban a diákoknak sokszor a papírsárkány jut eszébe és sajnos néhányan itt meg is állnak. Ennél azért pontosabb, precízebb fogalomalkotásra lenne szükség.
Ebben a cikkben megfogalmazzuk a deltoid precíz definícióját, végigvesszük a tulajdonságait. Megadjuk a kerület-, illetve területképletét és a végén a tanultak elmélyítésére megoldunk néhány feladatot.
Kinek hasznos az alábbi cikkünk?
Neked, ha általános iskolás vagy, és most ismerkedsz a négyszögfajtákkal.
Neked, ha érettségire készülsz, és nagyobb gyakorlatra szeretnél szert tenni geometriából.
Neked, ha esetleg már régebben voltál iskolás, ugyanakkor valamiért most szükséged lenne deltoidokkal kapcsolatos ismeretekre, és szeretnéd feleleveníteni azokat. Mi segítünk! Olvasd el cikkünket, és megtalálod a választ kérdéseidre.
A deltoid fogalma
A deltoid olyan négyszög, melynek két-két szomszédos oldala egyenlő.
Létezik konvex és konkáv deltoid is. Lásd az ábrát!
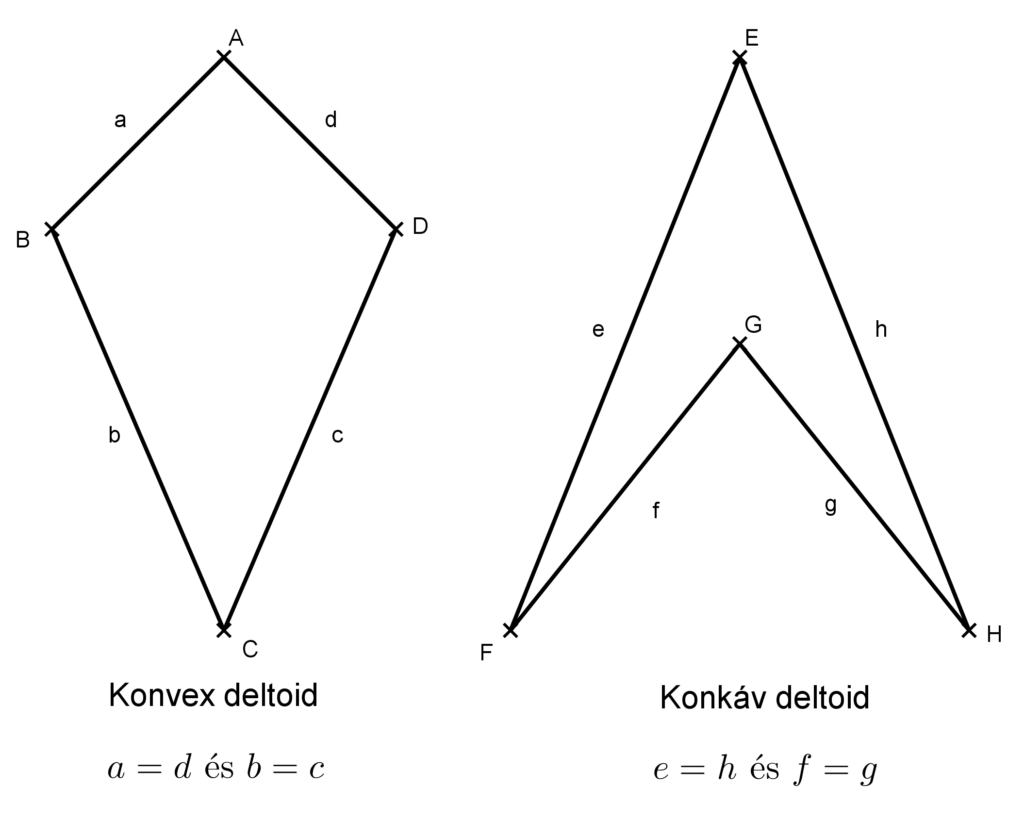
***
A deltoid két tulajdonsága
- 1. tulajdonság: A deltoid tengelyesen szimmetrikus négyszög.
Bizonyítás: Húzzuk be az ábrán látható ABCD deltoid BD átlóját! Ez a deltoidot két egyenlő szárú háromszögre bontja.
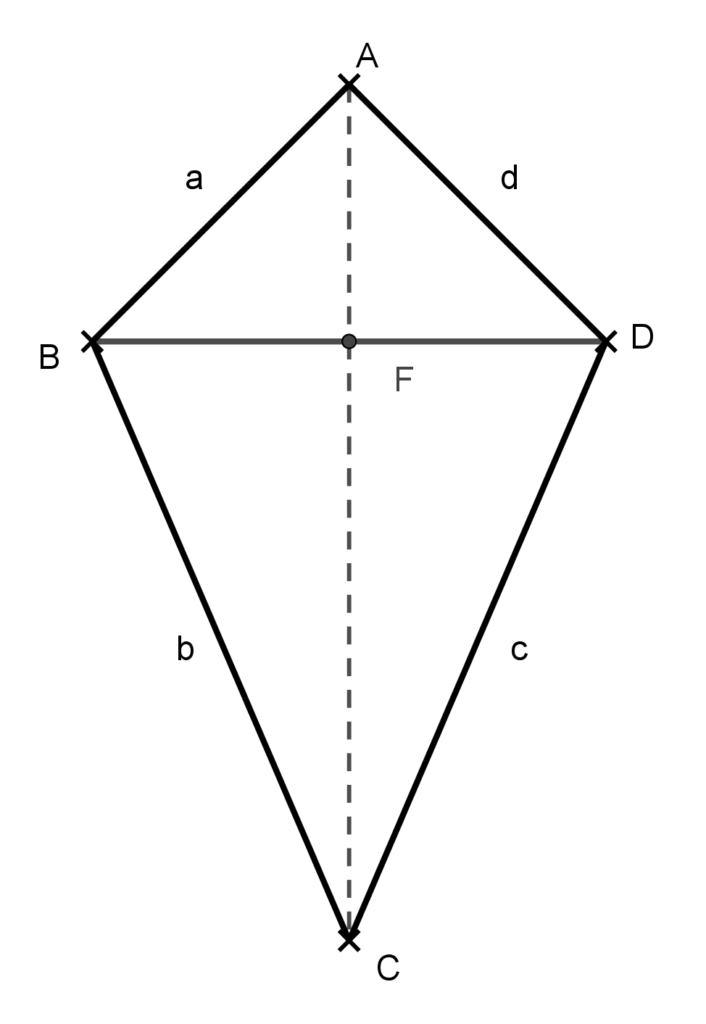
Kössük össze az átló F felezőpontját az A és C csúcsokkal. Az AF, illetve az FC szakasz rendre az ABD, illetve DBC háromszög alaphoz tartozó magassága. Ebből következik, hogy mindkettő merőleges a BD átlóra, így egy egyenesbe esnek, ami az AC átló egyenese.
Tehát az AC átló egyenese merőlegesen felezi a BD átlót, amiből következik, hogy a deltoidot az AC átlóra tükrözve az önmagába megy át, azaz az AC átló egyenese a szimmetria tengelye.
Hasonlóan végiggondolható konkáv deltoidra is. Ezt a tisztelt Olvasóra bízzuk. Ezzel a tételt bizonyítottuk.
***
- 2. tulajdonság: Ha egy négyszög szimmetrikus az egyik átló egyenesére, akkor az a négyszög deltoid.
Bizonyítás: Az ABCD négyszög szimmetria tengelye az AC átló egyenese. Ekkor a B és D csúcs egymásnak tengelyes tükörképe. Ebből következik, hogy AB=DA és BC=CD, azaz a négyszög két-két szomszédos oldala egyenlő, így deltoid.
***
A deltoid további tulajdonságai
Az alábbi két tulajdonság egyenes következménye az előzőekben bizonyítottaknak
- 3. tulajdonság: A deltoid átlói merőlegesek egymásra és a szimmetriaátló egyenese felezi a másik átlót.
- 4. tulajdonság: A deltoidnak van két egyenlő szöge. Ezek a szimmetriaátló két oldalán levő csúcsokhoz tartozó szögek.
***
A deltoid kerülete
Legyen adott az ABCD deltoid, melyben az oldalak hossza AB=DA=a és BC=CD=b. Ekkor a négyszög kerület hossza
K=2a+2b.
***
A deltoid területe
Tétel: A deltoid területét megkaphatjuk úgy, hogy két átlóhossza szorzatának a felét vesszük, azaz
T=\frac{e\cdot f}{2},ahol e és f a deltoid két átlójának a hossza.
Bizonyítás: A bizonyítást most konvex deltoidra hajtjuk végre. Ez alapján érdemes végiggondolni konkáv deltoidra is.
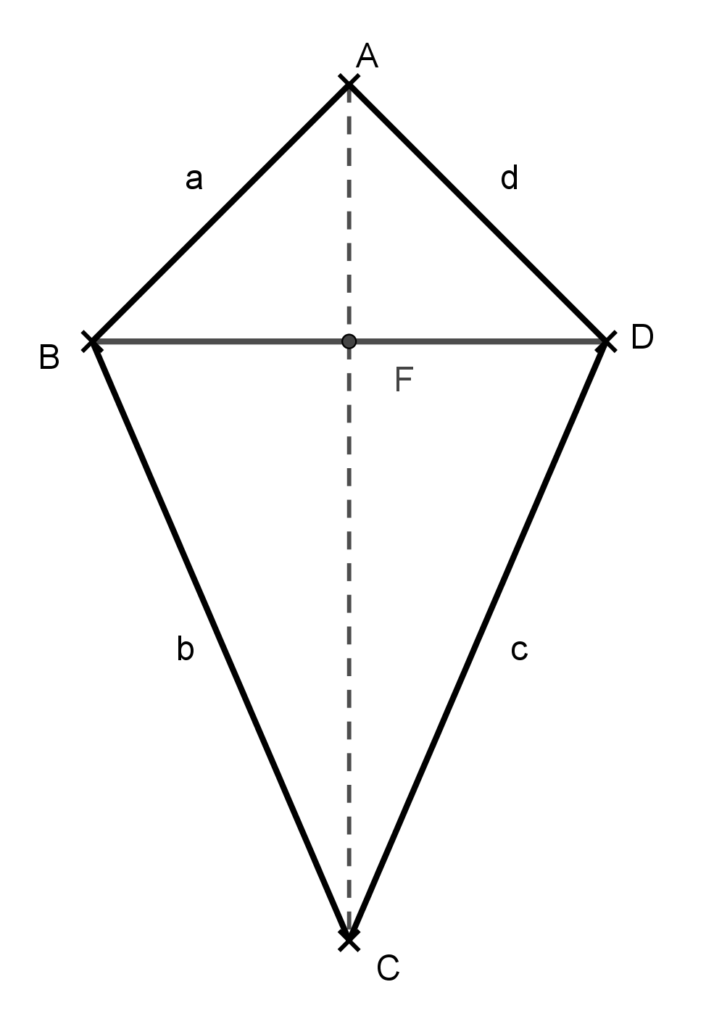
Legyen az ábrán látható konvex deltoid két átlójának a hossza BD=e és AC=f. Mint korábban már bizonyítottuk a két átló merőleges egymásra.
A konvex deltoid területét megkaphatjuk, ha az ABD és BCD háromszögek területének az összegét vesszük.
Így
T_{ABCD}=T_{ABD}+T_{BCD}=\frac{BD\cdot AF}{2}+\\+\frac{BD\cdot FC}{2}=\frac{BD\cdot (AF+FC)}{2}=\frac{e\cdot f}{2}.Ezzel a tételt bizonyítottuk.
Természetesen ez csak egy lehetséges módja annak, ahogy a deltoid területét kiszámíthatjuk. Nem kell ehhez ragaszkodni, mert lehet, hogy egy-egy konkrét esetben egyszerűbb módon is eljárhatunk.
***
Feladatok deltoidokra
Alapfeladatok
- 1. feladat: Az alábbi kijelentések közül melyik igaz, melyik hamis? Indokoljuk állításainkat!
- Egy deltoid szimmetriatengelye mindig átló.
- Ha egy deltoidnak van derékszöge, akkor a derékszögeinek a száma páros.
- Egy deltoidnak mindig van olyan átlója, ami egyben szögfelező is.
- Létezik olyan deltoid, melynek szemközti oldalai egyenlők.
Megoldás:
- Az állítás hamis, hisz a négyzet is deltoid és annak az oldalfelező merőlegesei is szimmetriatengelyei.
- Ez az állítás hamis, hisz lehet csak egy derékszöge a szimmetriaátló egyik végpontjánál lévő csúcsban.
- Ez igaz, hisz a szimmetriaátló egyben szögfelező is.
- Ez is igaz. A rombusz ilyen négyszög.
***
- 2. feladat: Egy deltoid két-két szemközti szögének összege egyenlő. két oldalának az aránya 5:12-höz, kerülete 68 cm. Mekkorák a deltoid oldalai? Mekkorák az átlói? Mekkora a területe?
Megoldás: Legyenek a deltoid csúcsai ABCD, ahol A és C a szimmetriaátló két csúcsa. Legyen AB=DA=a és BC=CD=b és a<b. A feltételek alapján a=5x és b=12x. Ennek felhasználásával felírhatjuk a kerületet
K=2a+2b=10x+24x=\\=34x=68.
Ebből kapjuk, hogy x=2, azaz a=10 cm, és b=24 cm.
Mivel a négyszög belső szögeinek összege 360° és ebben az esetben két-két szemközti szögének összege egyenlő, ezért a szemközti szögek összege 180°. Tudjuk, hogy a deltoid szimmetria átlójának két oldalán levő szögei egyenlők, ezért a B és D csúcsnál levő szögek 90°-osak. Készítsünk ábrát!
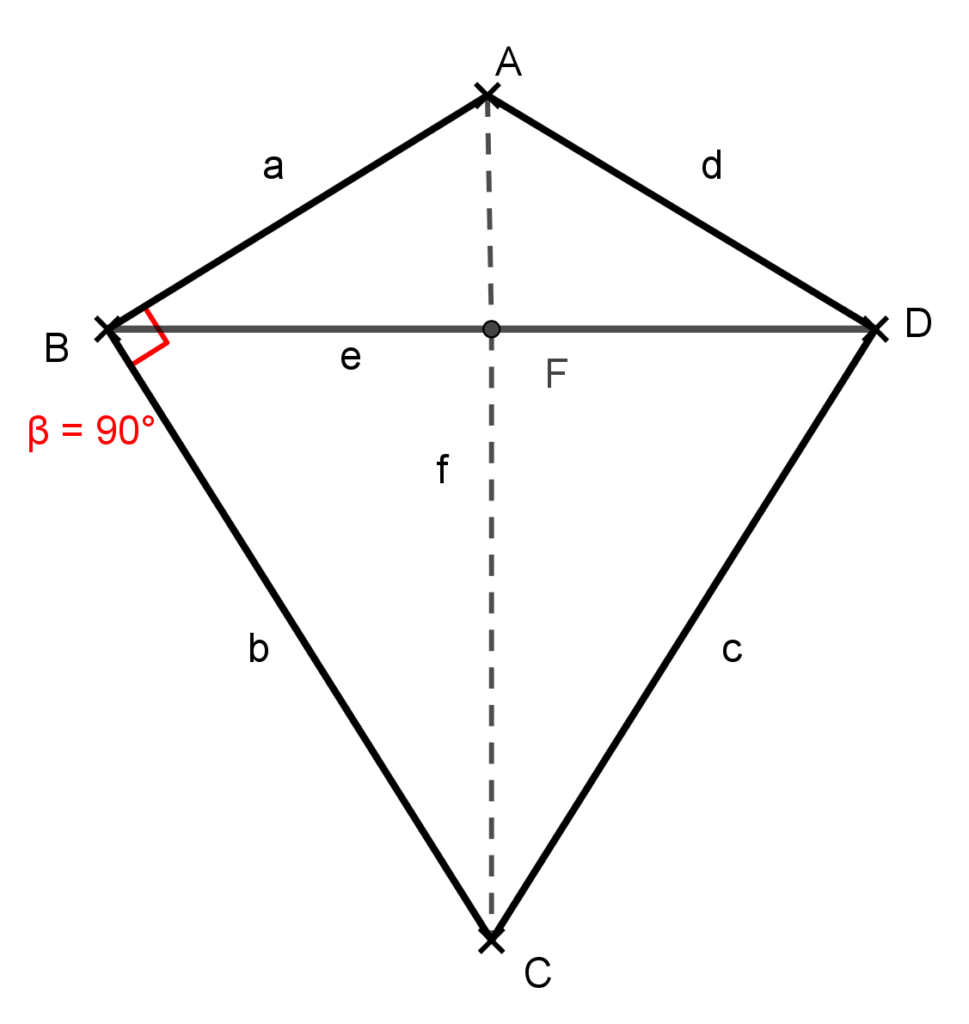
Mivel az ABC háromszög derékszögű, ezért a két befogója ismeretében kiszámolhatjuk a területét. A deltoid területét pedig megkaphatjuk ennek kétszereseként
T_{ABCD}=2T_{ABC}=2\cdot\frac{a\cdot b}{2}=\\=a\cdot b=10\cdot 24=240 \text{ }cm^2.Az f átlót az ABC derékszögű háromszögből számolhatjuk ki Pitagorasz-tétellel
f^2=a^2+b^2=10^2+24^2=676.
Ebből kapjuk, hogy f=26 cm.
Az e átlót úgy kaphatjuk meg legkönnyebben, ha felhasználjuk a deltoid már ismert területképletét, hisz a területét és az egyik átlóját már ismerjük.
Így
240=\frac{e\cdot 26}{2},ahonnan e=240/13 cm. Ezzel a feladatot megoldottuk.
***
Egyszerűbb feladatok
- 3. feladat: Számítsuk ki egy deltoid rövidebb átlóját és kerületét, ha hosszabbik átlója 60 cm hosszú, területe 600 cm2 és rövidebbik átlója a hosszabbat 2:3 arányban osztja!
Megoldás: Mivel a rövidebb átló 2:3 arányban osztja a hosszabb átlót, ezért a hosszabb átló a szimmetriaátló. Legyen az ABCD deltoid szimmetriaátlója AC=e=60 cm, a rövidebb átló BD=f. A területből és a hosszabb átlóból kiszámolhatjuk a rövidebb átlót
T=\frac{e\cdot f}{2}=\frac{60\cdot f}{2}.Innen kapjuk, hogy f=20 cm.
Készítsünk ábrát! Mivel BD az AC átlót 2:3 arányban osztja ezért AF=24 cm és FC=36 cm.
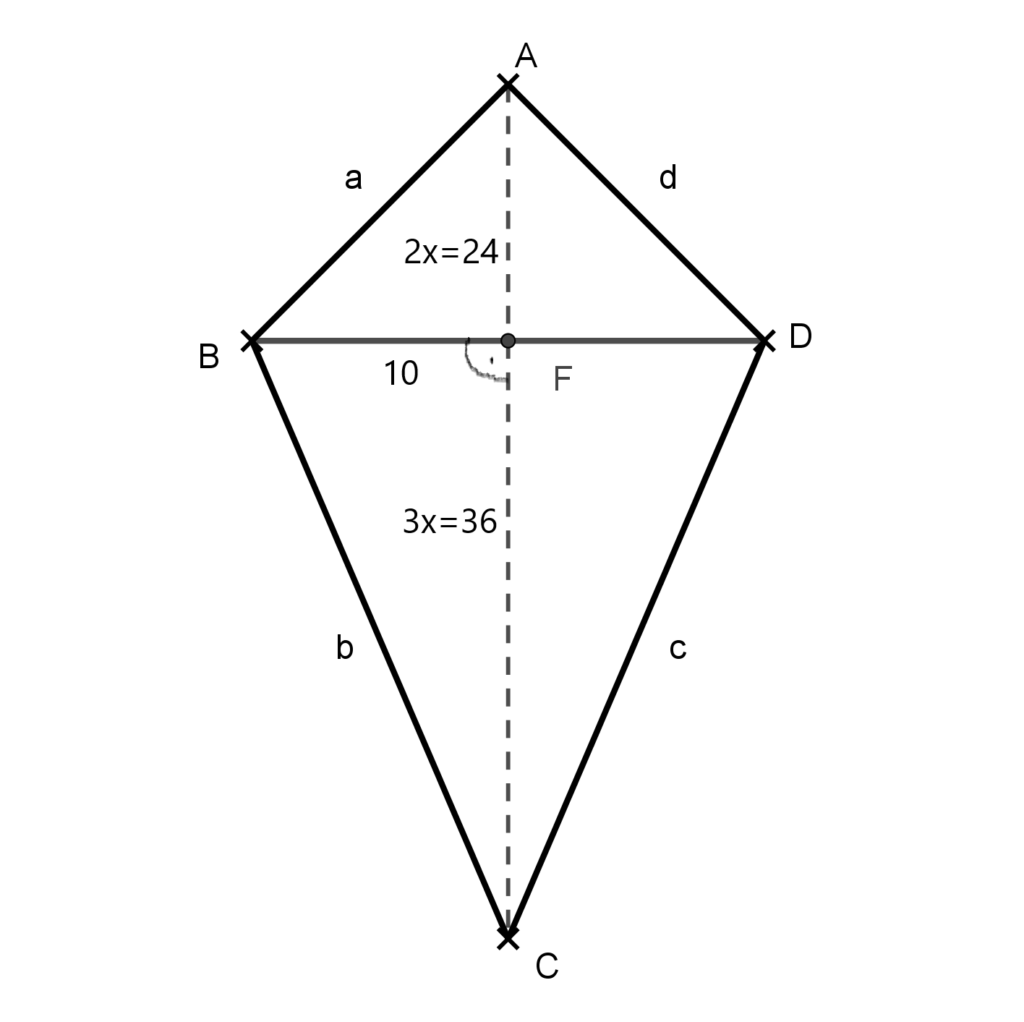
Számítsuk ki a deltoid oldalait. Használjuk ki, hogy az átlók a deltoidot négy derékszögű háromszögre bontják, melyek közül kettő-kettő egybevágó.
Az BFC háromszögben:
a^2=10^2+24^2=676.
Ebből a=26 cm.
A BFC háromszögben
b^2=10^2+36^2=1396.
Ebből b=37,36 cm két tizedes jegyre kerekítve.
Így a háromszög kerülete két tizedes jegyre kerekítve 126,72 cm. ezzel a feladatot megoldottuk.
***
A következő feladat előtt tisztázzuk az érintőnégyszög fogalmát. Az érintőnégyszög olyan négyszög, melynek oldalai egy adott kör érintői.
- 4. feladat: Bizonyítsuk be, hogy bármely konvex deltoid érintőnégyszög is egyben.
Bizonyítás: Ha valaki ismeri az érintőnégyszögek tételének megfordítását, akkor számára egyszerű a bizonyítás. A tétel úgy szól, hogy ha egy konvex négyszög szemközti oldalainak az összege egyenlő, akkor a négyszög érintőnégyszög. Ez nyilván teljesül bármely konvex deltoidra, hisz két-két szomszédos oldala egyenlő hosszú.
Most máshogy is bebizonyítjuk a problémát. Ahogy háromszög beírt körénél, úgy az érintőnégyszögeknél is a beírt kör középpontját a belső szögfelezők metszéspontja adja meg. Tehát elég azt bizonyítani, hogy a belső szögfelezők egy pontban metszik egymást.
Legyen az ABCD deltoid szimmetriaátlója AC, ami egyben az A és C csúcsnál levő szögének szögfelezője. Azt kell még belátni, hogy a másik két szög szögfelezője az AC átlón metszi egymást. Ez pedig következik abból, hogy a deltoid szimmetria tengelye AC, hisz erre tükrözve az ACB háromszöget a CDA háromszöget kapjuk. Lásd az ábrát!
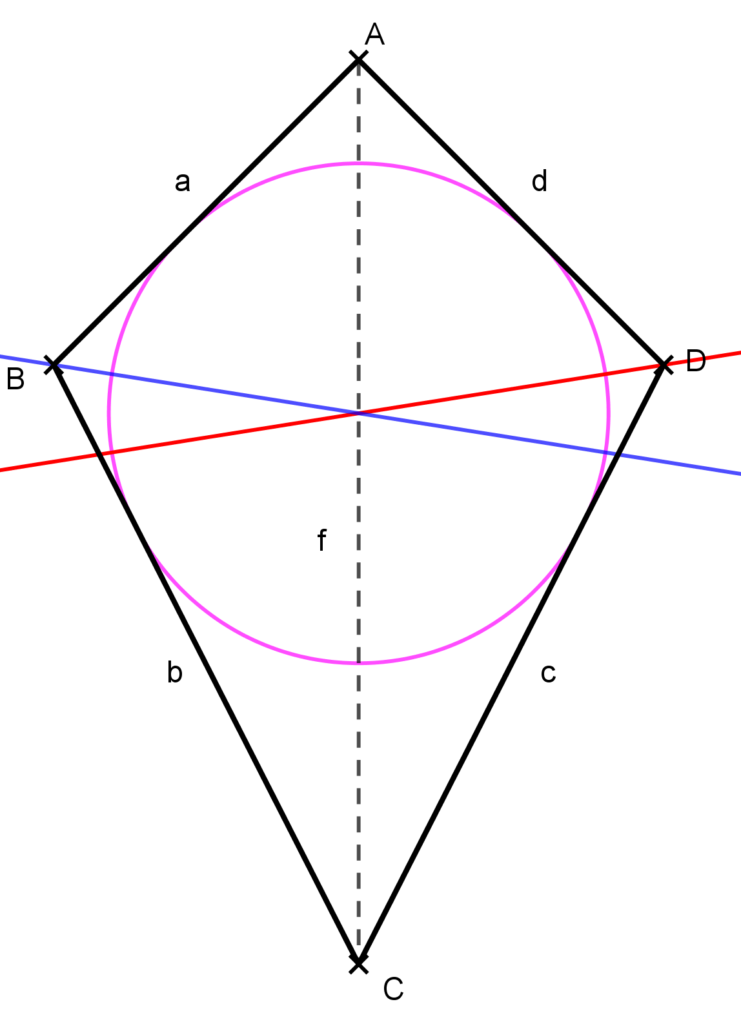
Ezzel az állítást bizonyítottuk.
***
Emelt szintű feladat
- 5. feladat: Egy húrdeltoid oldalainak az aránya 3:4-hez. Mekkora a beírt és a köré írt köre sugarainak az aránya?
Megoldás: Legyenek a deltoid csúcsai ABCD és szimmetriaátlója AC.
A húrdeltoid olyan deltoid, melynek van köré írt köre. Mivel a húrdeltoid és a kör is tengelyesen szimmetrikus, ezért a deltoid AC szimmetriaátlója egyben a kör átmérője is.
Mivel a B és D csúcs a körvonalán van és AC a kör átmérője, ezért az ABC háromszög olyan háromszög, melyben a köré írt kör középpontja az egyik oldal felezőpontja, amiből következik a Thalész-tétel megfordítása alapján, hogy a B csúcsnál derékszög van. Természetesen a D csúcsnál is. Készítsünk ábrát!
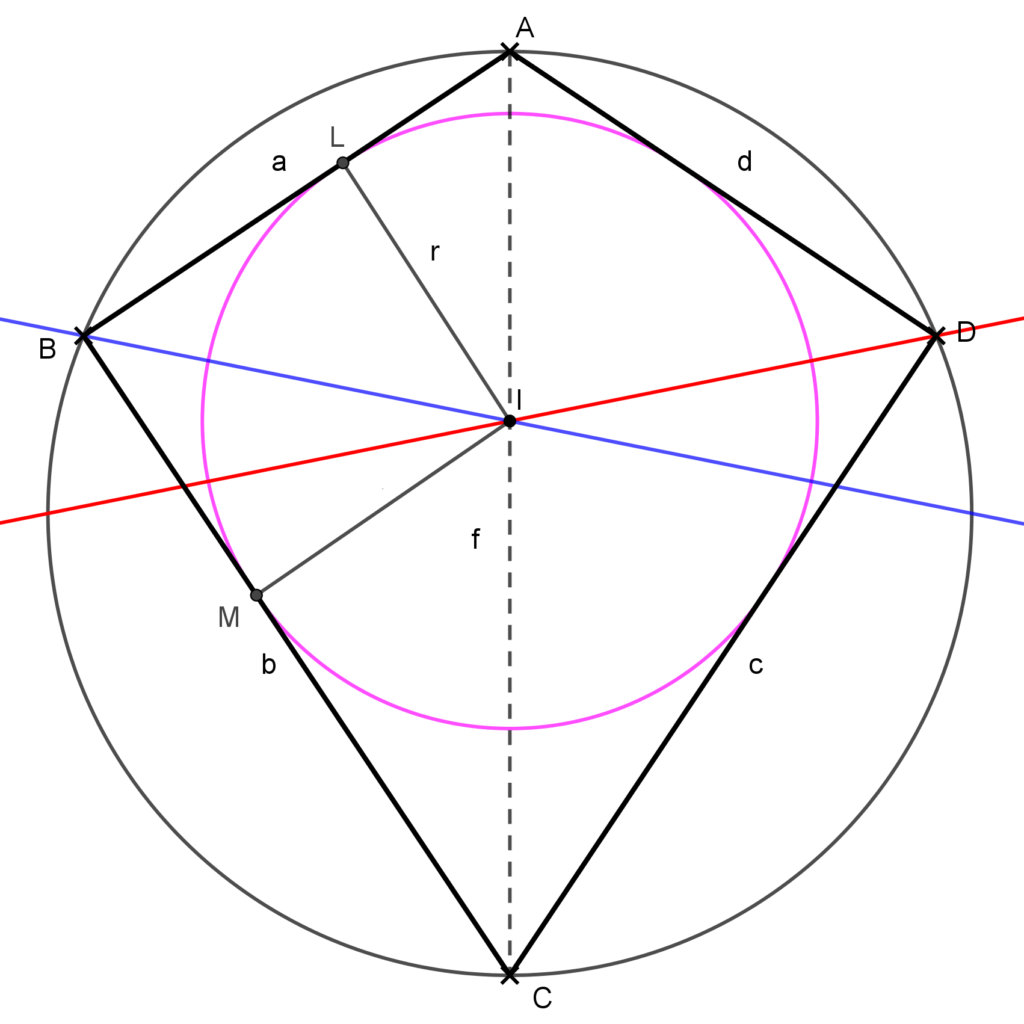
A köré írt kör R sugarát megkapjuk, ha az AC átlót kiszámoljuk. Írjuk fel Pitagorasz tételét és használjuk fel, hogy a:b=3:4,
AC^2=a^2+b^2=\\=(3x)^2+(4x)^2=25x^2.
Ebből AC=5x, így R=2,5x.
A beírt kör sugarának kiszámításához használjunk területképletet. Az ABC derékszögű háromszög területe egyrészt
T_{ABC}=\frac{a\cdot b}{2},másrészt összerakható a BCI és ABI háromszögek területéből.
Ennél a két háromszögnél húzzuk be az L és M érintési pontokba a beírt kör r sugarát. Ezek lesznek a háromszögek a, illetve b oldalához tartozó magasságai.
Így
T_{ABC}=T_{ABI}+T_{BCI}=\\=\frac{a\cdot r}{2}+\frac{b\cdot r}{2}=\frac{r\cdot (a+b)}{2}.Vessük össze a két területképletet
\frac{a\cdot b}{2}=\frac{r\cdot (a+b)}{2}.Így a beírt kör sugara
r=\frac{a\cdot b}{a+b}=\frac{3x\cdot 4x}{3x+4x}=\frac{12\cdot x}{7}.Tehát a két kör sugarának aránya
\frac{r}{R}=\frac{\frac{12x}{7}}{\frac{5x}{2}}=\frac{24}{35}.Ezzel a feladatot megoldottuk.
***
Összefoglalás
A fenti összeállításban definiáltuk a deltoidot, majd megismertük néhány tulajdonságát. Levezettük a deltoid kerület- és területképletét. Végül 5, fokozatosan nehezedő feladatban alkalmaztuk a tanult ismereteket.
Szeretnél még több, hasonló cikket olvasni? Akkor böngéssz a blogunkon Matekos blog!
Emelt szintű érettségire készülsz, vagy elsőéves egyetemista vagy? Ekkor ajánljuk figyelmedbe az online tanuló felületünket és a felkészülést segítő csomagjainkat. Az ezekkel kapcsolatos részletekről itt ÉrettségiPro+ olvashatsz.
Összegyűjtöttük az eddigi összes emelt szintű matematika érettségi feladatsort és a megoldásokat. Ezt a gyűjteményt, valamint az érettségire készüléssel kapcsolatos hasznos tanácsokat a Emelt szintű matematika feladatsorok linken érheted el.
Szerző: Ábrahám Gábor (szakmai önéletrajz)
Cikkek
A szerző további cikkei megtalálhatók a Budapesti Fazekas Milyály Gyakorló Általános Iskola és Gimnázium matematika oktatási portálján:
- Feladatok megoldása az analízis eszközeivel.
- Függvény és inverze egyenletekben
- A háromszög területe
- Polinomalgebrai feladatok
- Szélsőértékfeladatok megoldása elemi úton
Az emelt szintű érettségire készüléssel kapcsolatos írásaink a 34 hét alatt új tudás születik, illetve 17 fejezet matematikából linken érhetők el.
A szerző által írt tankönyvek a Maxim Kiadó linken találhatók.
További speciális négyszögekről (paralelogramma, rombusz) az alábbi cikkekben lehet olvasni Paralelogramma illetve Rombusz linken érhetők el.
Matek versenyre készülőknek
Ha olyan ambícióid vannak, hogy szeretnél matematikával versenyzés szintjén foglalkozni, akkor javaslom az Erdős Pál Matematikai Tehetségondozó Iskolát. Ezzel vonatkozó részletek ezen linken Erdős Pál Matematikai Tehetséggondozó Iskola olvashatók. A matematika versenyek témáit feldolgozó könyvek, kiadványok (a szerző Egyenlőtlenségek I.-II. című könyvei is) a MATE alapítvány, kiadványok linken kersztül vásárolhatók meg.

