A kör különlegesen fontos szerpet tölt be a hétköznapi életben, valamint a sík- és térgeometriában is. Ezért is elengedhetetlen, hogy részletesen tanulmányozzuk a vele kapcsoltos ismertekete. A kör területe és kerülete nemegyszer előkerül a mindennapi életben is. Elég, ha pl. a henger és a kúp felszínére, illetve térfogatára gondolunk. Hisz ott az alaplap kör.
Ebben a cikkben megismerkedünk a kör, a körvonal, a körlap, a körív, a körcikk és a körszelet definíciójával. Levezetjük a kör terület- és kerületképletét. Kiszámítjuk a körcikk és a körszelet területét. Az utolsó részben pedig 8 feladatban alkalmazzuk az ismereteket.
Kinek hasznos az alábbi cikkünk?
Neked, ha érettségire készülsz, és át szeretnéd ismételni a kör és részeivel kapcsolatos ismereteidet és rutint szeretnél szerezni a velük kapcsolatos feladatok megoldásában. Ehhez nyújt még segítséget az ÉrettségiPro+ tananyaga is, melyhez információkat ITT találsz.
Neked, ha esetleg már régebben voltál iskolás, ugyanakkor valamiért most szükséged lenne a körrel kapcsolatos ismeretekre, és szeretnéd feleleveníteni azokat.
Mi segítünk! Olvasd el cikkünket, és megtalálod a választ kérdéseidre.
A kör és részeinek definíciója
A körvonal és a körlap
A körvonal definíciója: A körvonal azon pontok halmaza a síkon, melyek egy adott ponttól, adott r távolságra vannak. Az adott pont a kör középpontja és az adott r távolság a kör sugara.
A körlap definíciója: A körlap azon pontok halmaza a síkon, melyek egy adott ponttól adott r távolságnál nem nagyobb távolságra vannak.
Körvív, körcikk
A körvonalat két pontja két körívre bontja. A körívek közös része a köríveket határoló két pont, a körívek közös végpontja. Az ábrán ez a két pont az A és B pont, az egyik körív pedig a piros színnel jelölt i ív.
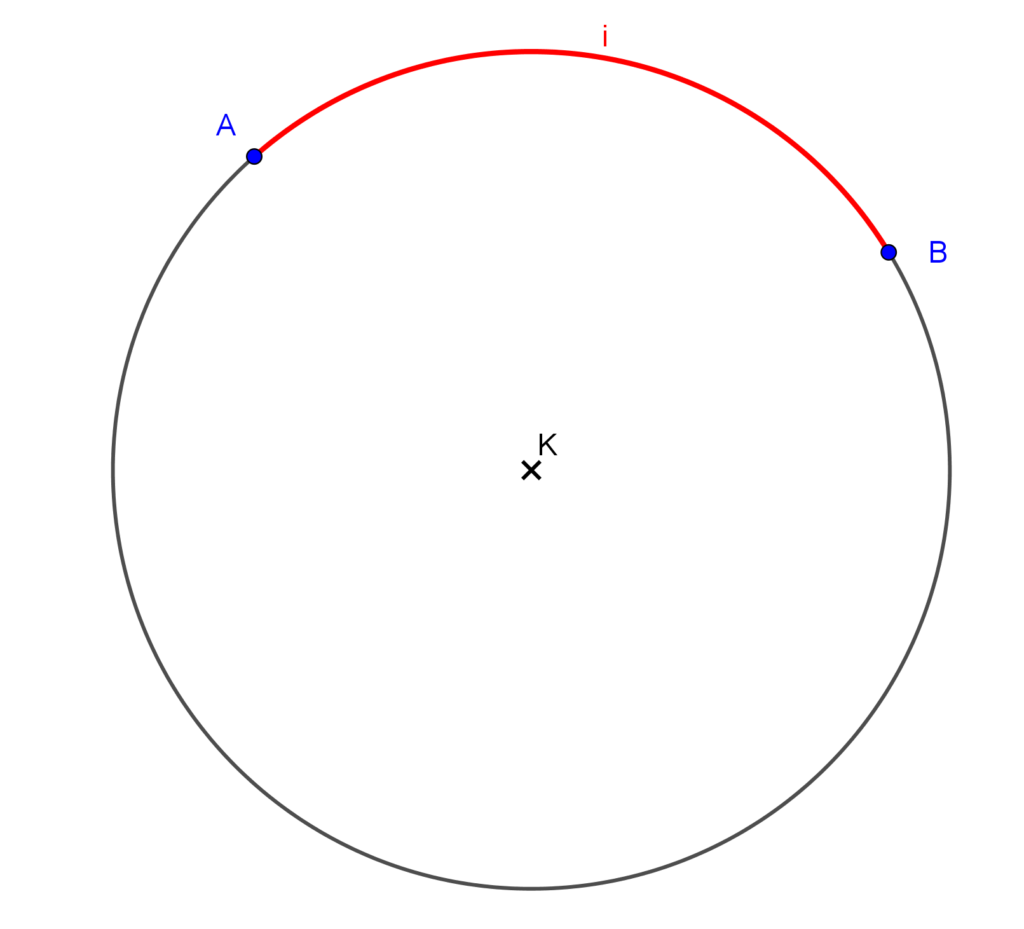
Ha összekötjük az A és B pontokat a kör K középpontjával, akkor az így kapott sugarak, illetve az i körív által határolt körlaprészt körcikknek nevezzük. Természetesen a két sugár valamint az A és B pontok közötti másik ív is határol egy körcikket. Az ábrán látható α és β szögeket, melyek csúcsa a kör középpontja, a két szára pedig a kör egy-egy sugara, középponti szögeknek nevezzük.
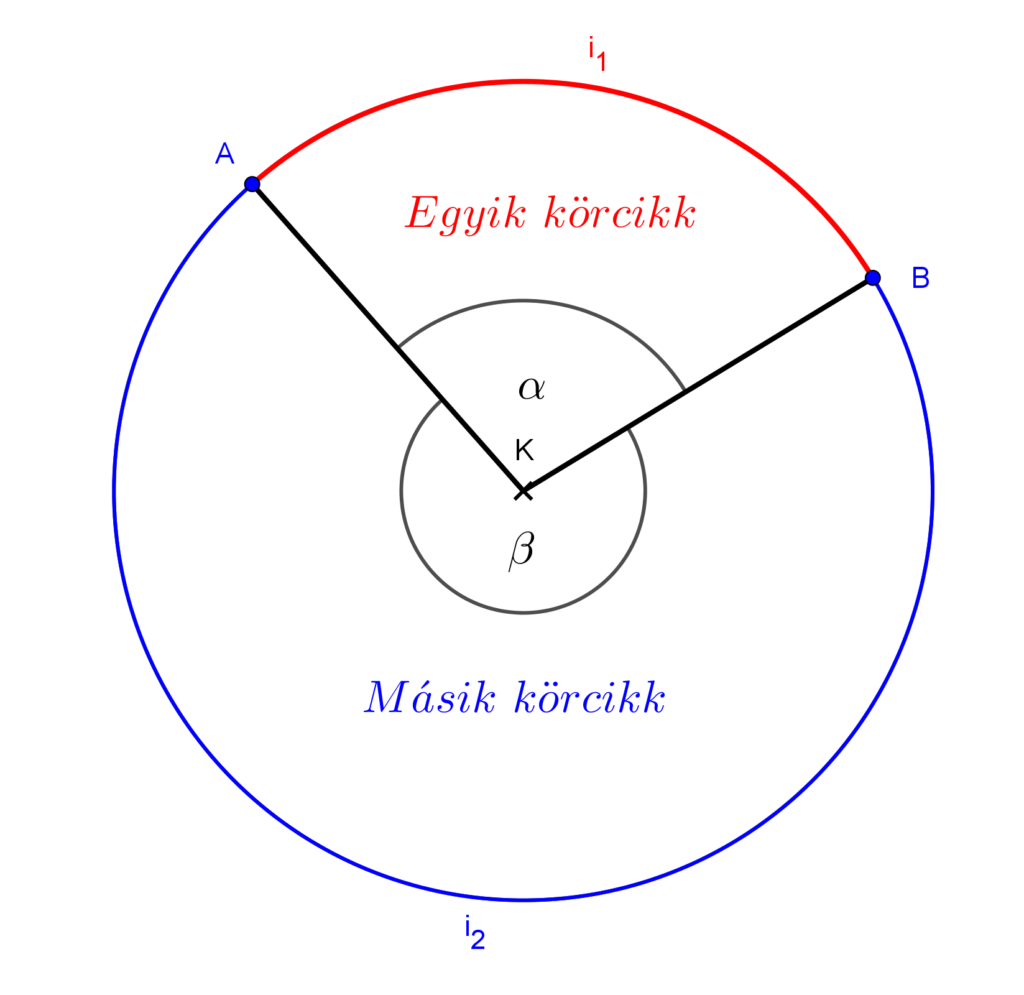
A kör szelője, húrja, a körszelet
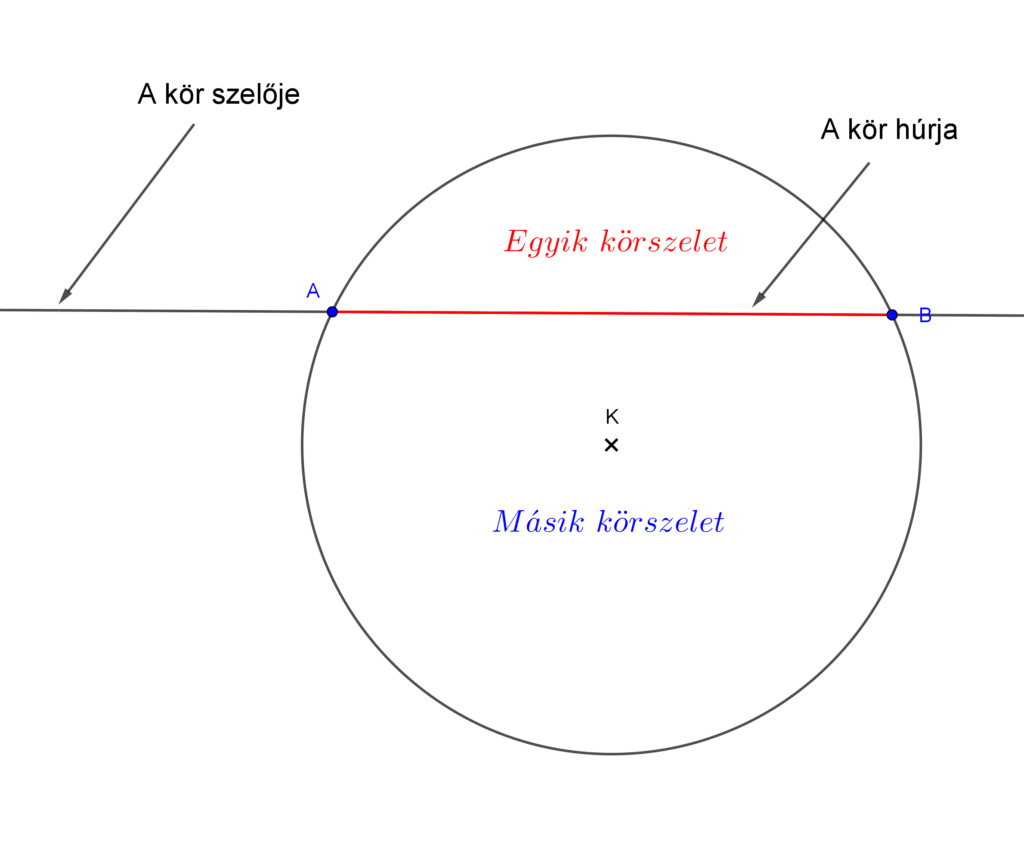
A körvonal két pontját összekötő egyenes a kör szelője. A szelő azon szakaszát, amelyik a két pont közé esik a kör húrjának nevezzük.
A kör húrja a körlapot két körszeletre bontja.
***
A kör területe
Tétel: Az r sugarhosszúságú kör területe
T=r^2\cdot \pi.
Bizonyítás: A tétel bizonyítása meghaladja a középiskolai középszintű követelményeket, még emelt szinten sem tekinthetjük kötlező ismeretnek. Ugyanakkor a levezetés az egyetmi tanulmányok szempontjából sok tanulságot rejt magában, ezért érdemes áttanulmányozni.
A bizonyításhoz a koordinátageometriai ismereteket és a határozott integrált használjuk.
Tekintsük az origó középpontú, r sugarú kört. Mint koordináta geometriából tudjuk, ennek egyenlete
x^2+y^2=r^2.
Készítsünk ábrát!
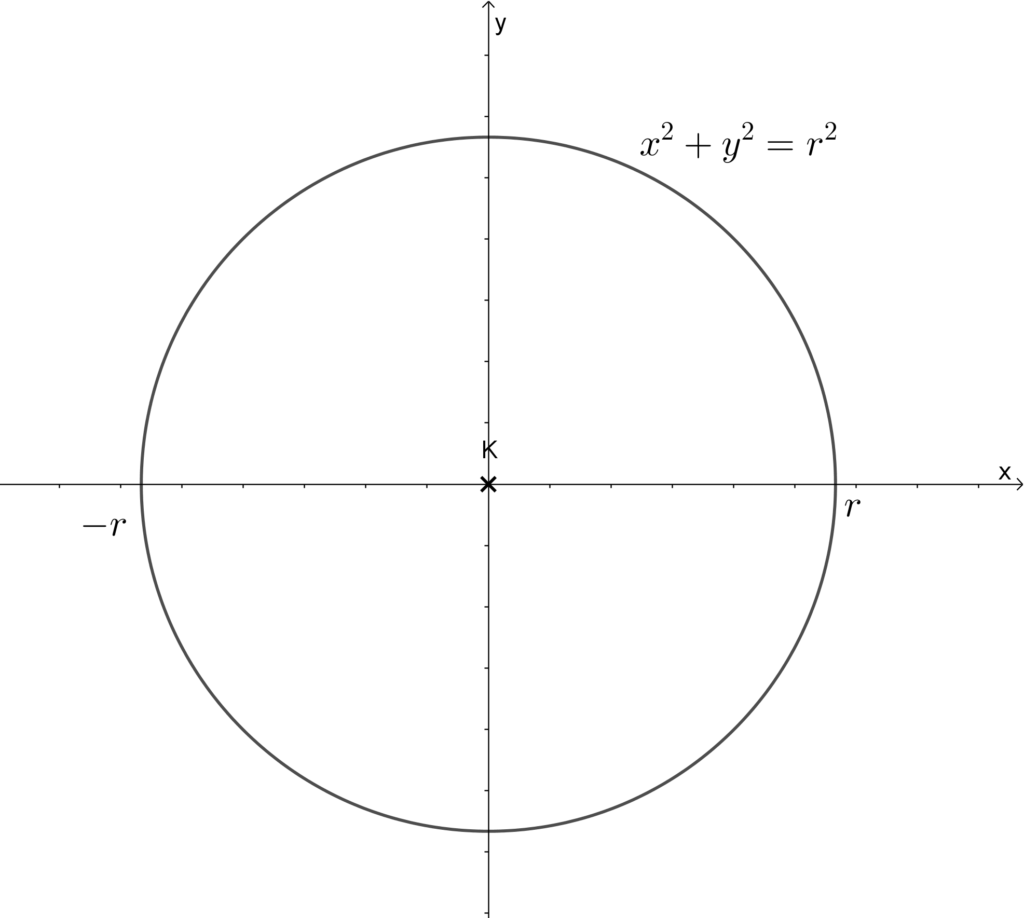
Elég csak a felső, azaz az x tengely feletti félkör területét meghatározni, majd a kapott értéket megszorozni kettővel.
A terület meghatározásához az
f:\text{ } [-r;r]\rightarrow [0;r];\text{ }f(x)=\sqrt{r^2-x^2}függvényt kell integrálnunk az értelmezési tartományán.
Tehát
T=2\int_{-r}^{r}\sqrt{r^2-x^2}dx.
Ezt az értéket helyettesítéssel való intágrálással határozzuk meg.
Ehhez felhasználjuk a helyettesítéses integrálás határozott integrálokra vonatkozó tételét.
Tétel: Tegyük fel, hogy g függvény diffrenciálható és g’ függvény integrálható az [a;b] intervallumon. Ha f folytonos a g értékkészletén, azaz a [g(a);g(b)] intervallumon, akkor
\int_{g(a)}^{g(b)}f(x)dx=\int_{a}^{b}f(g(t))\cdot g'(t)dt.Hogy alkalmazhatjuk ezt a tételt ebben az esetben?
Itt
f(x)=\sqrt{r^2-x^2}.Legyen
x=g(t)=r\cdot \text{cos}tekkor
f(g(t))=\sqrt{r^2-(g(t))^2}=\sqrt{r^2-r^2\cdot (\cos(t))^2}=r\cdot \sqrt{1-(\cos(t))^2}és
g'(t)=(r\cdot \text{cos}t)'=-r\cdot \text{sin}t.Az új integrációs határok:
r\cdot \text{cos}t=-r \Rightarrow \text{cos}t=-1 \Rightarrow t=\pi,és
r\cdot \text{cos}t=r \Rightarrow \text{cos}t=1 \Rightarrow t=0.Tehát
T=2\int_{-r}^{r}\sqrt{r^2-x^2}dx=-2r^2\int_{\pi}^{0}\sqrt{1-\cos^2t} \cdot \text{sin}t dt,mivel a [0;π] intervallumon a sint nemnegatív értékű, így
\sqrt{1-\cos^2t}=\sin t.Tehát
T=-2r^2\int_{\pi}^{0} \sin^2t dt.Az integrál kiszámításához használjuk fel, hogy
\sin^2t=1-\cos^2t
és a kétszeres szög koszinuszának addíciós tételének átrendezéséből
\cos2t=\cos^2 t-\sin^2t=1-2\sin^2t,
azaz
\sin^2t=\frac{1-\cos2t}{2}Így
T=-2r^2\int_{\pi}^{0} \sin^2t dt=2r^2\int_{0}^{\pi} \sin^2t dt=r^2\left(\int_{0}^{\pi}1dt-\int_{0}^{\pi}\cos2tdt\right)==r^2\left[t-\frac{1}{2}\sin2t\right]_{0}^\pi=r^2\left(\pi-\frac{1}{2}\sin2\pi-0+\frac{1}{2}\sin0\right)=r^2\pi.Ezt kellett bizonyítani.
***
A kör kerülete
A sokszögek kerületét ki tudjuk számolni, ha az oldalak hosszát összeadjuk. Hogyan határozhatjuk meg a kör kerületét?
A módszer lényege, hogy közelítsük két oldalról az r sugarú kör kerületét beírt, illetve köré írt szabályos sokszögek kerületével. A sokszögek oldalszáma legyen rendre:
2^2; \text{ } 2^3;\text{ } ...\text{ } 2^n.A kerületük pedig rendre
k_{2^2};\text{ } k_{2^3};\text{ } ... \text{ }k_{2^n},illetve
K_{2^2};\text{ } K_{2^3};\text{ } ...\text{ } K_{2^n}.Szemléltessük a kétoldali közelítést az alábbi ábrasorozattal:
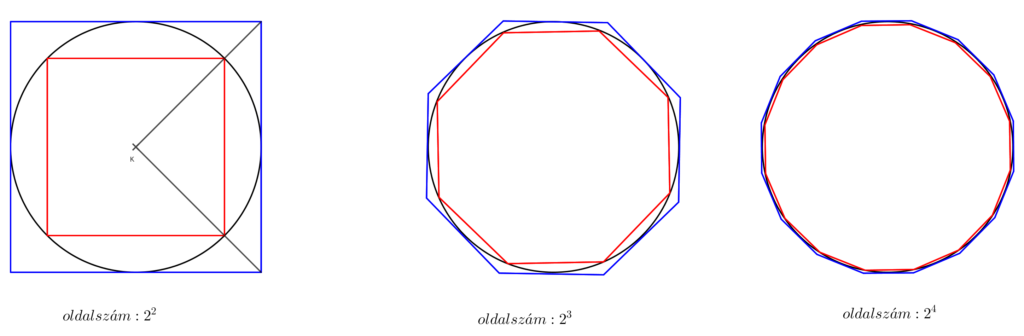
Be lehet bizonyítani, hogy
k_{2^n} < k_{2^{n+1}} \text{ és } K_{2^n} > K_{2^{n+1}},valamint az is könnyen látható, hogy
k_{2^{n+1}} < K_{2^n}.MIndezért természetesnek látszik, hogy a kör kerülete olyan szám, ami minden pozitív egész n esetén a
k_{2^n} \text{ és } K_{2^n} közé esik.
Mivel be lehet bizonyítani, hogy
K_{2^n}-k_{2^n} \rightarrow 0,így pontosan egy olyan szám van, ami minden pozitív egész n esetén
k_{2^n} \text{ és } K_{2^n} kerületértékek közé esik. Ezt a számot nevezzük a kör kerületének.
Ez a szám az r sugarú kör esetén a
K=2\cdot r\cdot \pi.
***
A kör részeinek területe, a körív hossza
A körcikk területe, a körív hossza
A körcikk területére és a körív hosszára vonatkozólag az alábbi tétel fogalmazható meg.
Tétel: Egy körben a középponti szögek nagysága és a hozzájuk tartozó körívek hossza, illetve körcikkek területei egyenesen arányosak.
A tétel bizonyításával nem fofglalkozunk, csak a következményeivel.
Az előző állítás lényegében azt mondja ki, hogy ha α és β a két középponti szög az adott körben, akkor
\frac{\alpha}{\beta}=\frac{i_{\alpha}}{i_{\beta}}=\frac{t_{\alpha}}{t_{\beta}}.Tekintsük ehhez az alábbi ábrát:
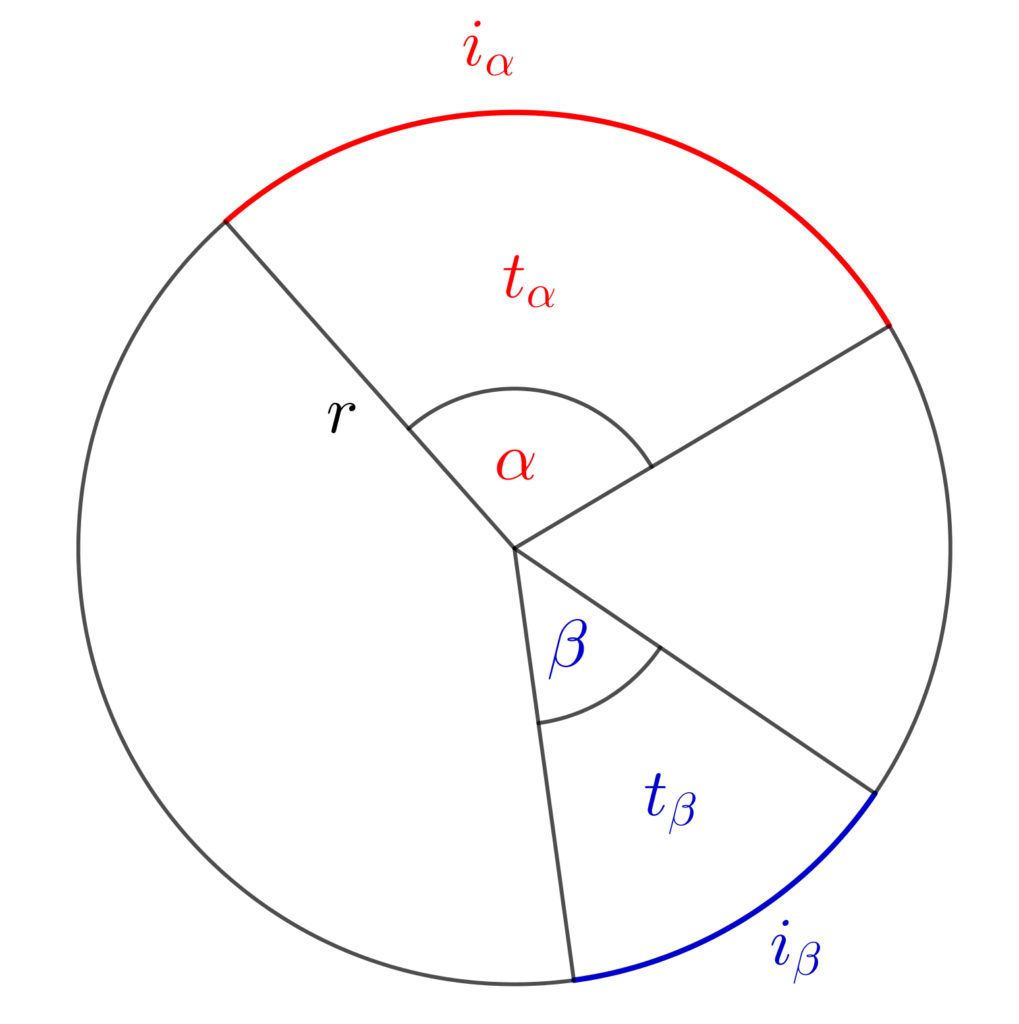
Mivel a 360°-os középponti szöghöz tartozó körív a kör kerülete, körcikk pedig a teljes kör, így
\frac{\alpha}{360°}=\frac{i_{\alpha}}{2r\pi}=\frac{t_{\alpha}}{r^2\pi},így
i_{\alpha}=\frac{\alpha}{180°}\cdot r\pi \text{ és } t_{\alpha}=\frac{\alpha}{360°}\cdot r^2\pi.Ebből a két képletből következik, hogy
t_{\alpha}=\frac{\alpha}{360°}\cdot r^2\pi=\frac{\alpha}{180°}\cdot r\pi\cdot\frac{r}{2}=\frac{i_{\alpha} \cdot r}{2}.***
A körszelet terület
Legyen adott az r sugarú kör, melynek húrjának két végpontja az α középponti szögű körcikket határozza meg. Lásd az ábrát!
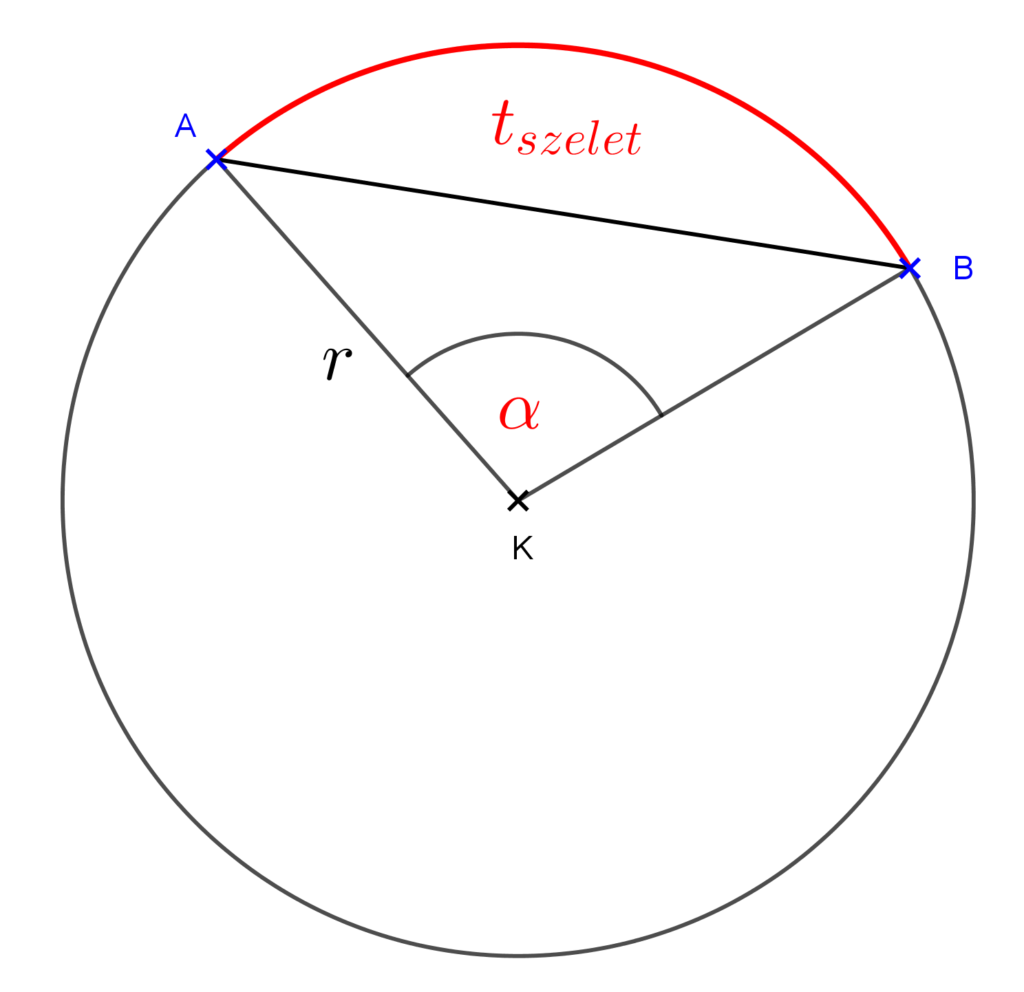
Az ábrán felvett kisebbik körszelet területét megkapjuk, ha az α középponti szögű körcikk területéből kivonjuk a KBA háromszög területét.
Tehát
t_{szelet}=t_{\alpha}-t_{KBA}=\frac{\alpha}{360°}\cdot r^2\pi-\frac{r^2\cdot \sin\alpha}{2}.Itt felhasználtuk a háromszög trigonometrikus területképletét. Erről a Háromszög területe című cikkünkben olvashatnak, amit a Háromszög területe linken lehet elérni.
***
Feladatok
Kör az alapfeladatokban
- 1. feladat: Az alábbi állítások közül melyik igaz, melyik hamis?
- Ha egy kör átmérőjét háromszorosára növeljük, akkor a kerülete is háromszorosára nő.
- Ha egy kör átmérőjét négyszeresére változtatjuk, akkor a területe négyszeresére változik.
- Ha egy körcikk területe ötöde a kör területének, akkor a körcikk középponti szöge 72°.
- Ha egy körcikk középponti szögét megkétszerezzük, akkor a körcikk területe négyszeresére nő.
Megoldás:
- Igaz, mivel a kör kerülete egyenesen arányos a kör átmérőjével.
- Hamis. Ha egy kör átmérőjét a négyszeresére változtatjuk, akkor a sugara is négyszeresére változik. Mivel a kör területe sugarának a négyzetével egyenesen arányos, így a terület tizanhatszorosára nő.
- Igaz, mivel a körcikk területe egyenesen arányos a körcikk középponti szögével.
- Hamis. Mivel a körcikk területe egyenesen arányos a középponti szögével, ezért a területe is kétszeresére nő.
***
- 2. feladat: A szegedi Fogadalmi templom toronyórájának nagymutatója 2,7 méter, kismutatója 2,1 méter hosszú. Mekkora utat tesz meg a két mutató végpontja 1 óra alatt?
Megoldás: A nagymutató végpontja egy óra alatt egy teljes kört tesz meg. Mivel a mutató hossza egyenlő a kör sugarával, így R=2,7 méter.
Így a nagymutató végpontja által megtett út két tizedesjegyre kerekítve:
K=2R\pi=2\cdot 2,7\cdot \pi \approx 16,96\text{ m}.A kismutató egy óra alatt egy teljes kör egytizenketted részét futja be, tehát egy olyan körcikk ívét, melynek középponti szöge a 360° tizenketted része, azaz 30°. A kör sugara a kismutató hossza, azaz r=2,1 méter.
Így a kismutató végpontja által megtett út két tizedesjegyre kerekítve:
i=\frac{1}{12}\cdot 2r\pi=\frac{r\pi}{6}\approx 0,55 \text{ m}.Ezzel a feladatot megoldottuk.
***
Könnyű feladatok
- 3. feladat:
- a) Mekkora az egységsugarú kör 270°-os középponti szögéhez tartozó ívének hossza? (középszintű matematika érettségi 2006. október 5. feladat)
- b) Egy kör sugara 6 cm. Számítsa ki ebben a körben a 120°-os középponti szöghöz tartozó körcikk területét! (középszintű matematika érettségi 2005. május 28. 4. feladat)
Megoldás:
a) A feltétel szerint a kör sugara r=1 egység és a körcikk középponti szög 270°. Használjuk a körív kiszámítására vonatkozó képletet:
i_{\alpha}=\frac{\alpha}{180°}\cdot r\pi=\frac{270°}{180°}\cdot 1\cdot \pi\approx 4,71 \text{ egység}.b) Ebben az esetben a kör sugara 6 cm és a körcikk középponti szöge 120°. Most a körcikk területének kiszámítására vonatkozó képletet használjuk:
t_{\alpha}=\frac{\alpha}{360°}\cdot r^2\pi=\frac{120°}{360°}\cdot 6^2\cdot\pi\approx37,70\text{ cm}^2.Ezzel a feladatokat megoldottuk.
***
- 4. feladat: Egy kör alakú szökőkút átmérője 6 méter. A szökőkutat körgyűrűszerűen veszi körbe egy d=2 méter széles virágágyás. Mekkora a virágágyás területe és ez hány százaléka a szökőkút területének? (A keresett értékeket két tizedesjegyre kerekítve adjuk meg! )
Megoldás: Mivel a szökőkút átmérője 6 méter, ezért a sugara 3 méter. Készítsünk ábrát!
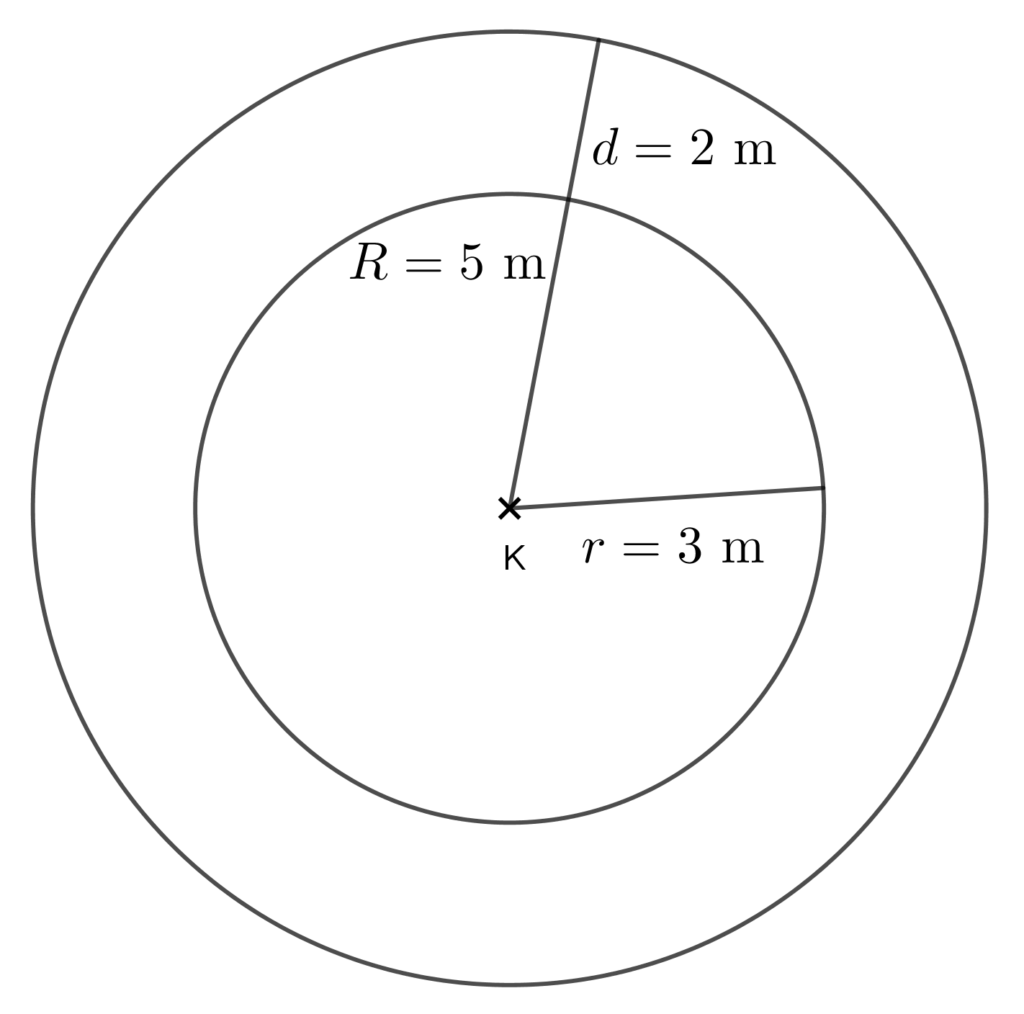
A virágágyás, azaz a körgyűrű területét megkapjuk, ha a nagy kör területéből kivonjuk a kis kör területét:
T=R^2\cdot\pi--r^2\cdot\pi=25\pi-9\pi\approx50,27\text{ m}^2.A szökőkút területe:
t=r^2\pi=9\pi\approx28,27\text{ m}^2.Most határozzuk meg, hogy a virágágyás területe hány százaléka a szökőkút területének. Ehhez segítséget nyújt a százalékszámításról szóló cikkünk, ami a Százalékszámítás linken érhető el.
Mivel
p=\frac{T}{t}\cdot100=\frac{50,27}{28,27}\cdot100\approx177,79,így a virágágyás területe a szökőkút területének a 177,79 %-a.
Ezzel a feladatot megoldottuk.
***
Kör a közepes nehézségű feladatok
Körív hossza, körcikk területet
- 5. feladat: Egy 30 cm sugarú kör középpontjától 50 cm-re levő pontból érintőket húzunk a körhöz. Mekkora annak zárt a síkidomnak a területe és kerülete, melyet a két érintő és az érintési pontok által meghatározott kisebbik körív határol?
Megoldás:
Készítsünk ábrát! Vegyük fel az érintőket és húzzuk be a sugarakat az érintési pontokba.
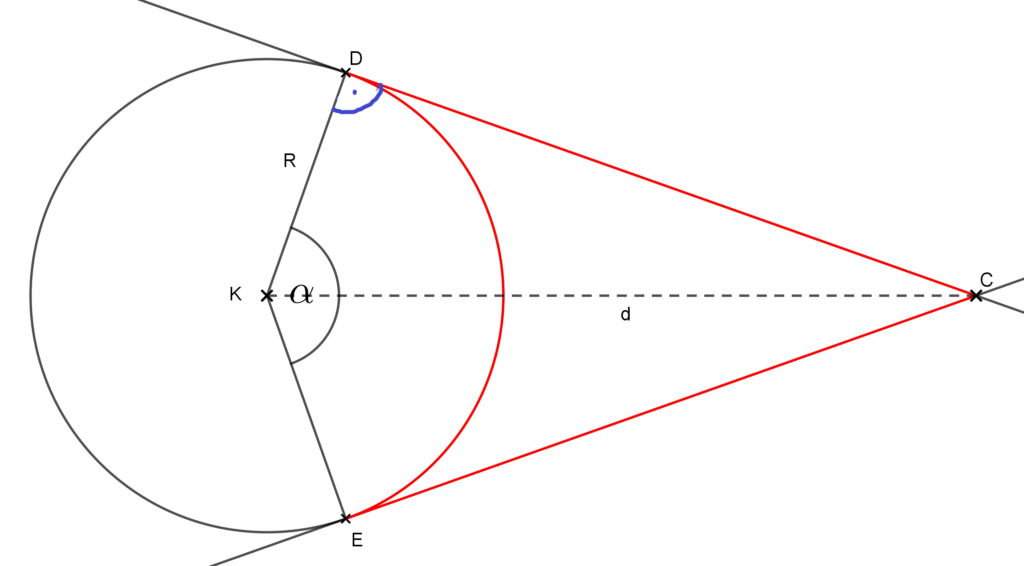
A feladat a piros színnel jelölt szakaszok, illetve körív által határolt síkidom területét és kerületét kérdezi. Mivel a külső pontból körhöz húzott érintő szakaszok egyenlő hosszúak (CD=EC), valamint KD=EK=R, ezért a KECD négyszög deltoid. A deltoidokkal kapcsolatos ismereteket lásd a deltoidokról szóló cikkünkben, mely a Deltoid fogalma, tulajdonságai linken érhető el.
Tudjuk, hogy az érintési pontba húzott sugár merőleges az érintőre, így a D és E csúcsnál derékszög van. Ha kiszámoljuk a deltoid területét és abból kivonjuk az α középponti szögű körcikk területét, akkor megkapjuk a kérdezett területet.
A deltoidot a KC szakasz két egybevágó derékszögű háromszögre bontja. Ezek területének összege egyenlő a deltoid területével.
Először számoljuk ki a derékszögű háromszög ismeretlen befogóját, ami megegyezik az érintő hosszával. A számításhoz használjuk Pitagorasz-tételét. Az ezzel kapcsolatos ismeretek a Pitagorasz-tételről szóló cikkünkben olvashatók a Pitagorasz-tétel linken.
Így
CD^2=KC^2-R^2=50^2-30^2=1600,
tehát CD=40 cm.
Ebből kiszámolhatjuk a deltoid területét
T_{KECD}=2\cdot\frac{R\cdot DC}{2}=R\cdot DC=1200 \text{ cm}^2.Az α középponti szögű körcikk területéhez határozzuk meg az α-t. A szög felét kiszámolhatjuk a KCD derékszögű háromszögből szögfüggvények felhasználásával:
\cos\frac{\alpha}{2}=\frac{R}{KC}=0,6.Ebből α=106,26°.
Így a körcikk területe:
T_{\alpha}=\frac{\alpha}{360°}\cdot R^2\pi\approx 834,57\text{ cm}^2.A keresett terület
T=T_{KECD}-T{\alpha}=365,43 \text{ cm}^2.A kerülethez ki kell számolni a DE kisebbik körív hosszát, ami
i_{\alpha}=\frac{\alpha}{180°}\cdot R\pi\approx 55,64\text{ cm}.A síkidom kerülete tehát
K=2\cdot DC+i_{\alpha}=135,46\text{ cm}.
Ezzel a feladatot megoldottuk.
***
Körszelet területe
- 6. feladat: Az előző feladatban szereplő körben mekkora a DE húr által levágott kisebbik körszelet területe?
Megoldás: Készítsünk egy újabb ábrát! Vegyük fel a DE szakaszt!
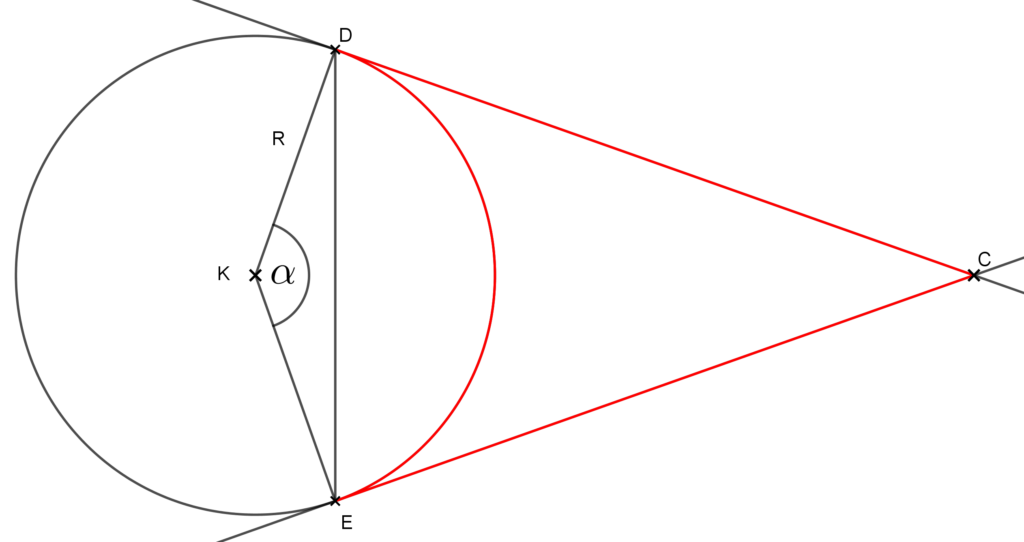
A kisebbik körszelet területét megkapjuk, ha az α középponti szögű körcikk területéből kivonjuk az EDK háromszög területét.
Az EDK háromszögből ismerünk két oldalt, ez a KE és a DK, illetve az általuk bezárt szöget, ezért a trigonometrikus területképlettel kiszámolhatjuk a területét. Az ezzel kapcsolatos ismeretek a Háromszög területe című cikkünkben olvashatók a Háromszög területe linken.
A körszelet területe:
T=\frac{\alpha}{360°}\cdot R^2\pi-\frac{R^2\cdot \sin\alpha}{2}\approx834,57-432=402,57\text{ cm}^2.Ezzel a feladatot megoldottuk.
***
Kör az emelt szintű feladatok
Körszelet területe
- 7. feladat: (2007. október emelt szintű érettségi 2. feladat) Egy családnak olyan téglalap alakú telke van, melynek két szomszédos oldala 68 m, illetve 30 m hosszú. A telek egyik sarkánál úgy rögzítettek egy kerti locsoló berendezést, hogy a telek rövidebb oldalától 4 m-re, a vele szomszédos oldaltól 3 m-re legyen. A locsoló berendezés körbe forgó locsolófeje azt a részt öntözi, amely a rögzítés helyétől legalább 0,5 m-re, de legfeljebb 4 m-re van. A telek mekkora területű részét öntözi a locsoló berendezés, és ez hány százaléka a telek területének?
Megoldás: A feladat részletes megoldása az alábbi videón látható.
***
Körív hossza
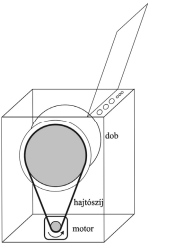
- 8. feladat: (2013. május emelt szintű érettségi 2. feladat) Az ábrán egy mosógép vázlatos rajza látható. A kisebb, 1cm sugarú kerék a motor tengelyéhez kapcsolódik, és egy hajtószíj segítségével forgatja meg a mosógép dobjához rögzített, 20 cm sugarú kereket, amitől a dob és benne a ruhák forognak mosás közben. A két kerék tengelye párhuzamos és a tengelyek távolsága 46 cm. (A hajtószíj a tengelyekre merőleges síkban van.) Milyen hosszú a feszes hajtószíj?
Megoldás: Készítsünk ábrát!
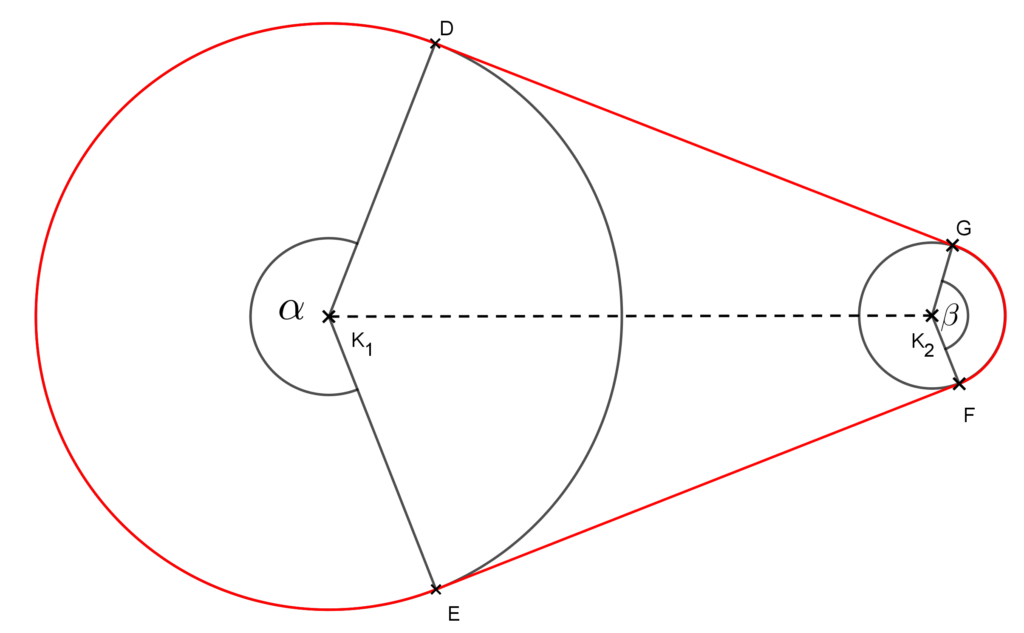
A feladatban szereplő hajtószíj hossza egyenlő az ábrán pirossal jelölt vonal hosszával, azaz az α és β középponti szögű körív, illetve az EF és GD közös külső érintőszakaszok hosszának összegével.
Először számoljuk ki az érintő szakaszok hosszát. Ehhez húzzunk párhuzamost a K1K2 szakasszal F érintési ponton keresztül és használjuk ki, hogy az érintési pontba húzott sugár merőleges az érintőre, azaz az E pontnál derékszög van. Lásd az alábbi ábrát!
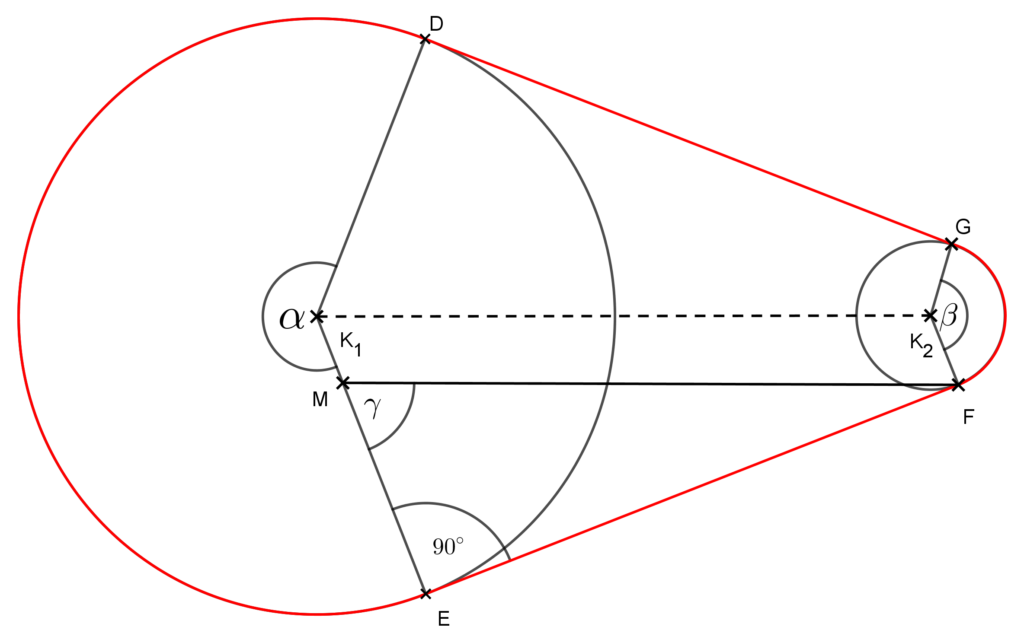
Az EF szakasz hosszát az EFM derékszögű háromszögből számolhatjuk ki, ahol FM=K1K2=46 cm, mert az MFK1K2 négyszög paralelogramma, hisz szemközti oldalai párhuzamosak és EM=R-r=20-1=19 cm.
Alkalmazzuk Pitagorasz tételét:
EF^2=FM^2-EM^2=46^2-19^2=1755,
azza GD=EF=41,89 cm.
Mivel egyállású szögek, ezért
\gamma=K_2K_1E\sphericalangle.
Ezért ha kiszámoljuk a γ szöget, akkor abból megkapjuk az α szöget is, hisz
\alpha=360°-DK_1E\sphericalangle=360°-2K_2K_1E\sphericalangle=360°-2\gamma.
A γ-t pedig az EFM derékszögű háromszögből kapjuk meg szögfüggvény használatával ugyanis
\cos\gamma=\frac{ME}{FM}=\frac{19}{46},így γ=65,6°, tehát α=228,8°.
Egyben megkaptuk a β szöget is, hisz az egyállású a DK1E szöggel, így β=2γ=131,2°.
A két körív hossza:
i_1=\frac{\alpha}{180°}\cdot R\pi=\frac{228,8°}{180°}\cdot 20\pi\approx79,59\text{ cm},i_2=\frac{\beta}{180°}\cdot r\pi=\frac{131,2°}{180°}\cdot 1\pi\approx2,29\text{ cm}.A hajtószíj hossza:
h=i_1+EF+i_2+GD=79,59+41,89+2,29+41,89=165,66\text{ cm}.***
Összefoglalás
A fenti cikkben megadtuk a kör területét és kerületét. Megismertük a körcikk és körszelet területének kiszámítási módját és a körív hosszának kiszámítását. Először egyszerűbb, majd nehezebb feladatokon keresztül alkalmaztuk a tanult ismereteket.
Szeretnél még több, hasonló cikket olvasni? Akkor böngéssz a blogunkon Matekos blog! Emelt szintű érettségire készülsz, vagy elsőéves egyetemista vagy? Ekkor ajánljuk figyelmedbe az online tanuló felületünket és a felkészülést segítő csomagjainkat. Az ezekkel kapcsolatos részletekről itt ÉrettségiPro+ olvashatsz.
Összegyűjtöttük az eddigi összes emelt szintű matematika érettségi feladatsort és a megoldásokat. Ezt a gyűjteményt, valamint az érettségire készüléssel kapcsolatos hasznos tanácsokat a Emelt szintű matematika feladatsorok linken érheted el.
Szerző: Ábrahám Gábor (szakmai önéletrajz)
Cikkek
A szerző további cikkei megtalálhatók a Budapesti Fazekas Milyály Gyakorló Általános Iskola és Gimnázium matematika oktatási portálján:
- Feladatok megoldása az analízis eszközeivel.
- Függvény és inverze egyenletekben
- A háromszög területe
- Polinomalgebrai feladatok
- Szélsőértékfeladatok megoldása elemi úton
Az emelt szintű érettségire készüléssel kapcsolatos írásaink a 34 hét alatt új tudás születik, illetve 17 fejezet matematikából linken érhetők el.
A szerző által írt tankönyvek a Maxim Kiadó linken találhatók.
Matek versenyre készülőknek
Ha olyan ambícióid vannak, hogy szeretnél matematikával versenyzés szintjén foglalkozni, akkor javaslom az Erdős Pál Matematikai Tehetségondozó Iskolát. Ezzel vonatkozó részletek ezen linken Erdős Pál Matematikai Tehetséggondozó Iskola olvashatók. A matematika versenyek témáit feldolgozó könyvek, kiadványok (a szerző Egyenlőtlenségek I.-II. című könyvei is) a MATE alapítvány, kiadványok linken kersztül vásárolhatók meg.

