Paralelogramma: feladatok egyszerűtől az emelt szintig

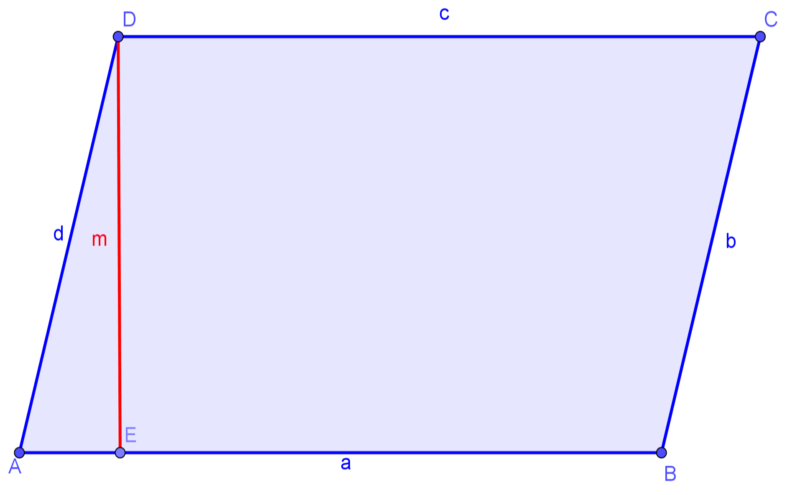
Ebben a cikkben alkalmazzuk a Paralelogramma: tulajdonságok, terület, kerület című cikkünkben szereplő elméleti ismereteket, melyet ITT olvashatsz. A legegyszerűbb, elemi feladatoktól indulva jutunk el az emelt szintű feladatokig. Az itt tárgyalt problémákban foglalkozunk a paralelogramma területével, kerületével és tulajdonságaival.

Kiknek ajánljuk ezt a cikket?

Nem csak azok figyelmébe ajánljuk az alábbi cikket, akik emelt szintű matematika érettségire készülnek. Hasznos lehet azok számára is, akik úgy érzik, geometriából hiányosságaik vannak és ezért szeretnének jártasságot szerezni ebben a témakörben. Ugyancsak hasznos lehet azoknak is, akik középszintű érettségire készülnek matematikából.

10 feladat paralelogrammákra

Alapfeladat

• 1. feladat: Az alábbi kijelentések közül melyik igaz, melyik hamis. Indokoljuk meg állításunkat.

1. Ha egy négyszög két átlója egyenlő, akkor az a négyszög paralelogramma.
2. Létezik olyan paralelogramma, melynek átlói merőlegesek egymásra.
3. A paralelogramma átlója egyben szögfelező is.
4. Létezik olyan paralelogramma melynek egyik oldala és a hozzá tartozó  magassága egyenlő.
5. Létezik olyan paralelogramma, melynek pontosan két derékszöge van

Válaszok:

1. Az állítás hamis. Ha egy négyszög átlói nem felezik egymást, akkor nem paralelogramma. Az ábra elkészítését a tisztelt Olvasóra bízzuk.
2. Az állítás igaz. Ilyen négyszög a rombusz, mint speciális paralelogramma. Lásd az erre vonatkozó blogunkat.
3. Az állítás hamis. Ha a paralelogramma két szomszédos oldala nem egyenlő, akkor az átló nem szögfelező. Lásd a 3. tulajdonságnál szereplő ábrát.
4. Az állítás igaz. Például a négyzet.
5. Az állítás hamis. Mivel a paralelogramma bármely oldalán fekvő két szögének az összege 180°, ezért a másik két szög is 90°nagyságú kell, hogy legyen.

***

Alapfeladat a paralelogramma kerületére, területére

• 2. feladat: Egy paralelogramma két szögének aránya 1:2, a kerülete 24 cm. Mekkorák az oldalai, ha egyik átlója egyenlő az egyik oldalával?

Megoldás: Legyen az ABCD paralelogramma kisebbik szöge az A, nagyobbik a B csúcsnál levő α, illetve β szöge. A feltétel szerint α:β=1:2 . Mivel az összegük 180°, így

\alpha +\beta =\alpha +2\alpha =3\alpha =180{}^\circ .

Ebből α=60° és β=120°. Készítsünk ábrát.

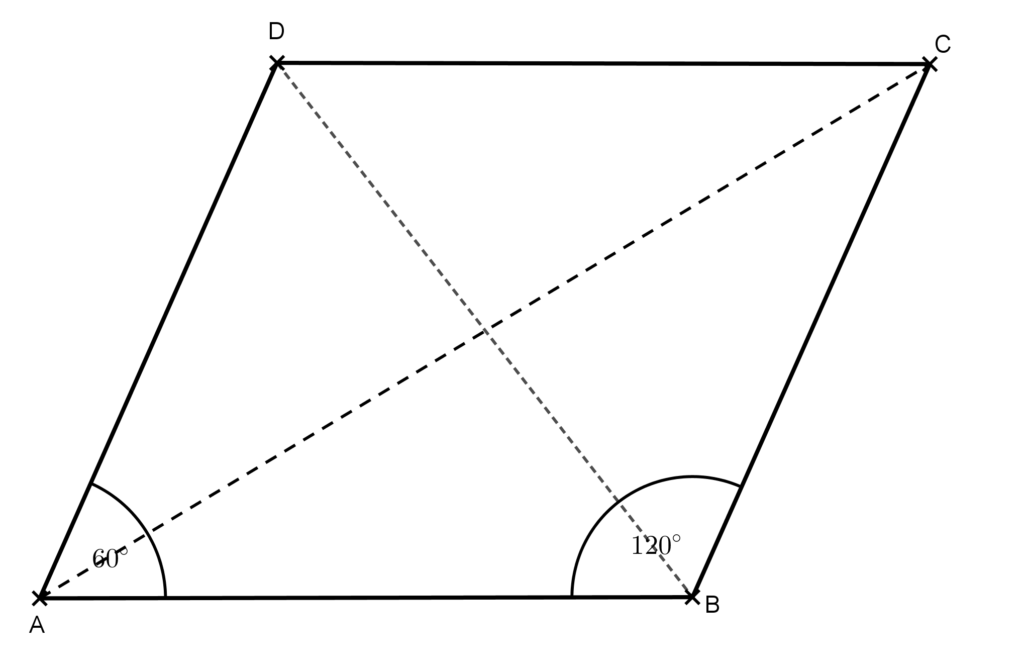
Az ABC háromszögben a B csúcsnál levő szög 120°, így a paralelogramma AC átlója hosszabb az oldalainál. Ebből következik, hogy csak a BD átló lehet egyenlő az egyik oldalával. Ez azt jelenti, hogy az ABD háromszög egyenlő szárú. Mivel az egyik szöge 60°, ezért szabályos is.

Így az oldalai egyenlők, azaz az ABCD négyszög rombusz. Mivel a kerülete 24 cm, ezért egy oldala ennek negyedrésze, azaz 6 cm. Ezzel a feladatot megoldottuk.

***

Nehezebb feladat a területére

• 3. feladat: Egy paralelogramma kerülete 112 cm, az oldalainak aránya 2:5-höz. Mekkora a paralelogramma területének pontos értéke, ha az egyik szöge harmada egy másik szögének?

Megoldás: Legyen az ABCD paralelogramma két oldalának hossza a és b, ahol a:b=2:5. Ekkor a=2x és b=5x, így

K=2a+2b=4x+10x=14x=112,

ebből x=8. A paralelogramma oldalai AD=a=16 cm és AB=b=40 cm.

Legyen a kisebbik szög az A csúcsnál lévő α szög, míg a nagyobb a B csúcsnál lévő β szög.  Ekkor

\alpha +\beta =\alpha +3\alpha =4\alpha =180{}^\circ .

Ebből α=45° és β=135°. Készítsünk ábrát, melyben vegyük fel célszerűen a 40 cm-es oldalhoz tartozó magasságot.

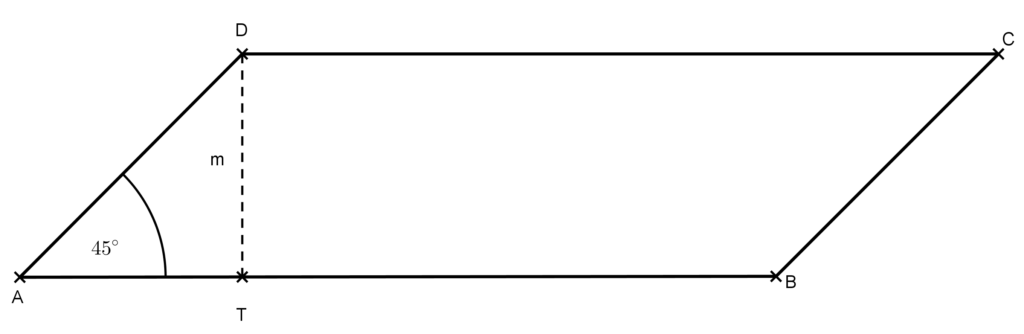
A paralelogramma területének kiszámításához meg kell határozni a az m magasságot. Mivel az így keletkező ATD derékszögű háromszög  A csúcsánál levő szöge 45°-os, így a háromszög egyenlő szárú, AT=m.

Alkalmazzuk Pitagorasz tételét erre a háromszögre:

{{m}^{2}}+{{m}^{2}}=A{{D}^{2}}, \text { azaz } 2{{m}^{2}}=256.

Innen

m=8\sqrt{2}.

A paralelogramma területe

T=b\cdot m=40\cdot 8\sqrt{2}=320\sqrt{2}c{{m}^{2}}.

Ezzel a feladatot megoldottuk.

***

• 4. feladat: Az ábrán látható paralelogrammában az azonos színnel jelölt szakaszok egyenlők. Mekkora az α szög?

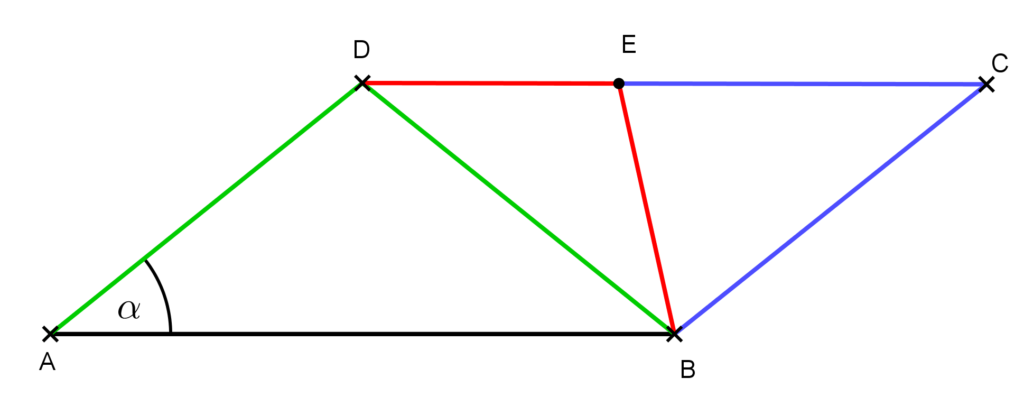
Megoldás: Mivel AD=BD, ezért

ABD\sphericalangle =\alpha .

Az EDB szög váltó szöge az ABD szögnek, így

EDB\sphericalangle =ABD\sphericalangle =\alpha.

A feltétel szerint DE=EB, így

DBE\sphericalangle =EDB\sphericalangle =\alpha.

Mivel a DBC háromszög  E-nél levő külső szöge egyenlő a nem mellette fekvő két belső szög összegével, ezért

CEB\sphericalangle =2\alpha .

Az EC és a BC szakaszok egyenlőségéből jön, hogy

EBC\sphericalangle =2\alpha .

Tudjuk, hogy az ABCD négyszög paralelogramma, ezért

BCD\sphericalangle =\alpha .

Készítsünk ábrát!

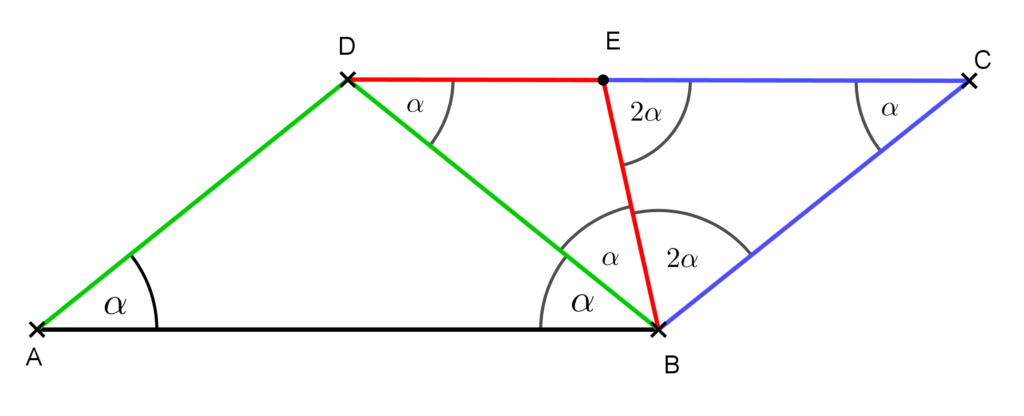
Ezek után az EBC háromszögeire írjuk fel, hogy

2\alpha +2\alpha +\alpha =180{}^\circ.

Ebből kapjuk, hogy α=36°. Ezzel a feladatot megoldottuk.

***

Feladat a háromszög középvonalára

A következő feladatban a háromszögek középvonalával foglalkozunk. Egy háromszögben két oldal felezőpontját összekötő szakaszt a háromszög középvonalának nevezzük.

• 5. feladat: Bizonyítsuk be, hogy a háromszög két oldalának felezőpontját összekötő középvonala párhuzamos a harmadik oldallal és fele akkora!

Megoldás: Tekintsük az ABC háromszög AC oldalának E felezőpontját a BC oldalának F felezőpontjával összekötő középvonalát! Tükrözzük a háromszöget az F pontra az ábrának megfelelően.

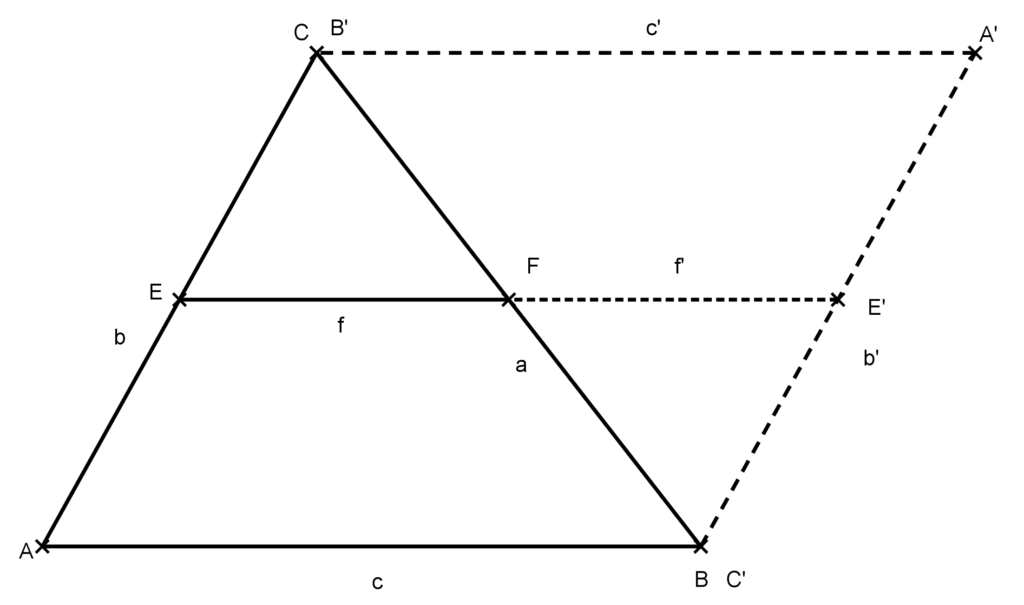
A tükrözés után kapott ABA’C négyszög középpontosan szimmetrikus, ezért paralelogramma. Mivel az EF középvonal F pontra vonatkozó tükörképe az FE’ szakasz, ezért az E, F és E’ pontok egy egyenesre esnek és E’ a BA’ szakasz felezőpontja, hisz az E pont az AC szakasz felezőpontja.

Ebből következik, hogy egyrészt az EE’ szakasz kétszerese az EF szakasznak, másrészt az EE’ szakasz a paralelogramma középvonala. Arról viszont már bizonyítottuk, hogy párhuzamosan egyenlő a másik két oldallal, azaz EE’ párhuzamos és egyenlő az AB oldallal. Így EF párhuzamos a c oldallal és fele akkora. Ezt kellett bizonyítani.

Megjegyzés: Egy háromszögnek három középvonala van. Ez a három szakasz a háromszöget négy egybevágó háromszögre bontja, melyek oldalai feleakkorák, mint az eredeti háromszög oldalai és egynek a területe az eredeti háromszög területének a negyedével egyenlő. Lásd az ábrát.

***

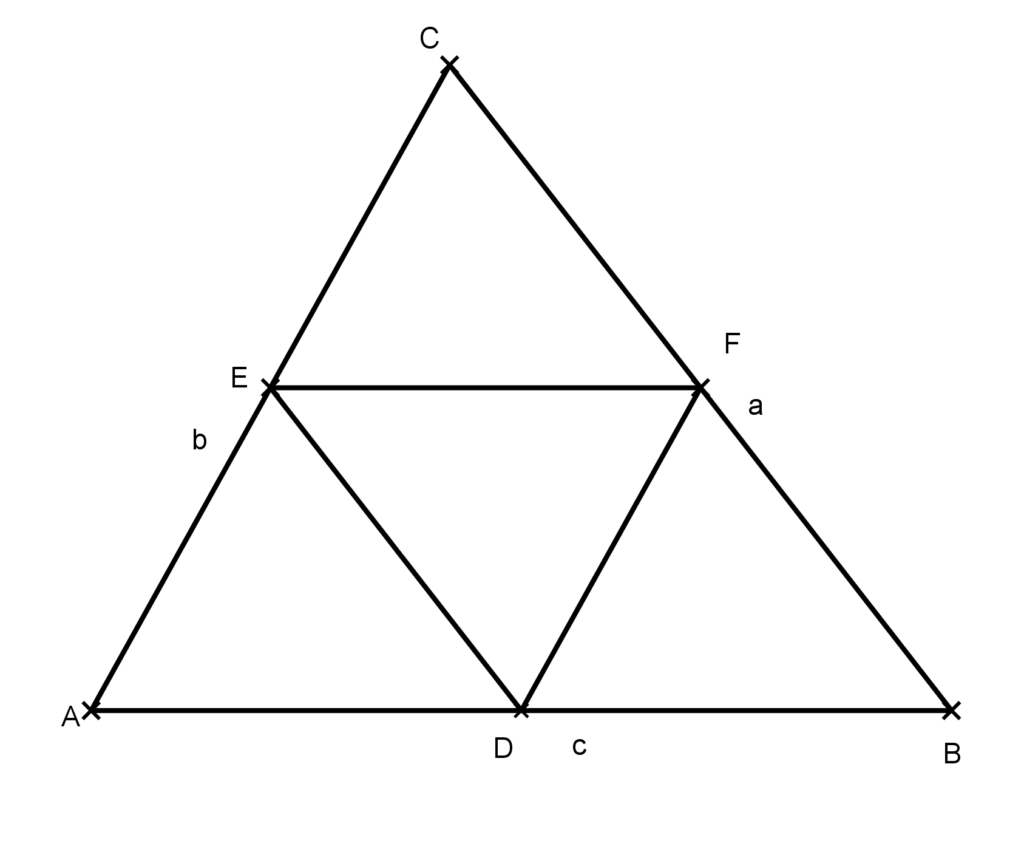
Feladat a négyszög középvonalára

• 6. feladat: Bizonyítsuk be, hogy a négyszög középvonalai felezik egymást! (Pierre Varignon 1731.)

Megoldás: Legyen az ABCD négyszög AB oldalának felezőpontja E, BC oldaláé F, CD oldaláé G és DA oldaláé H. Azt kell bizonyítani, hogy EG felezi FH-t. Mivel ez a két szakasz az EFGH négyszög két átlója, így a paralelogrammák 5. tulajdonsága alapján elég azt bizonyítani, hogy az EFGH négyszög paralelogramma.

Ehhez pedig elég azt belátni, hogy két szemközti oldala párhuzamos és egyenlő. Vegyük fel az EH és FG szakaszokat, valamint húzzuk be a BD átlót az ábrának megfelelően.

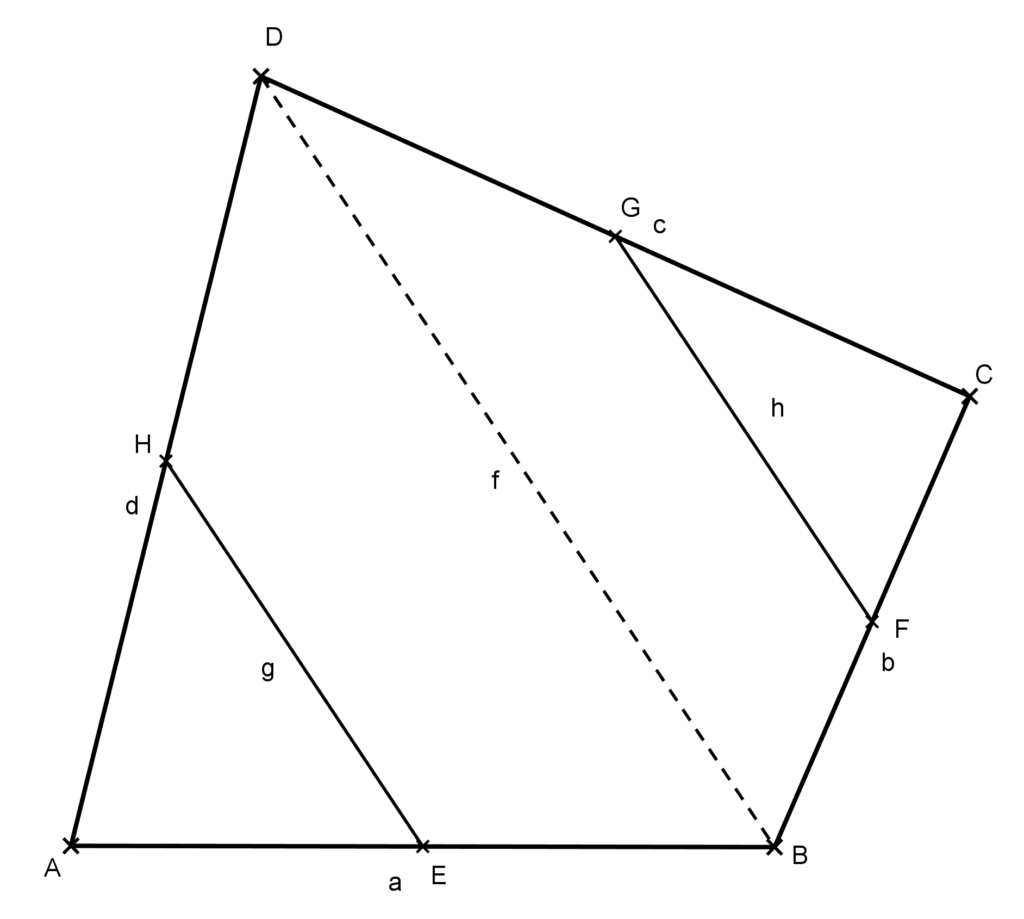
Az átló a négyszöget két háromszögre bontja. Ezekben az EH, illetve az FG szakasz egy-egy középvonal, így párhuzamos a harmadik oldallal és fele akkora. Tehát EH és FG párhuzamos BD és fele a BD-nek. Ebből következik, hogy EFGH négyszög paralelogramma, ezért EH felezi FG-t.

Az ábrán konvex négyszög szerepel, ugyanakkor a levezetés során sehol sem használtuk ki ezt a tulajdonságát. A bizonyítás ugyanígy végrehajtható konkáv négyszögre is. Ennek meggondolását a Tisztelt Olvasóra bízzuk. Ezzel a feladatot megoldottuk.

***

Játék a paralelogramma területével

• 7. feladat: Hányadrésze az ABCD négyszög oldalfelező pontjai által meghatározott négyszög területe az ABCD területének?

Megoldás: Használjuk fel az előző feladatban bizonyítottakat úgy, hogy az EFGH paralelogrammán kívüli négyszög rész területét számoljuk ki. Készítsünk ábrát!

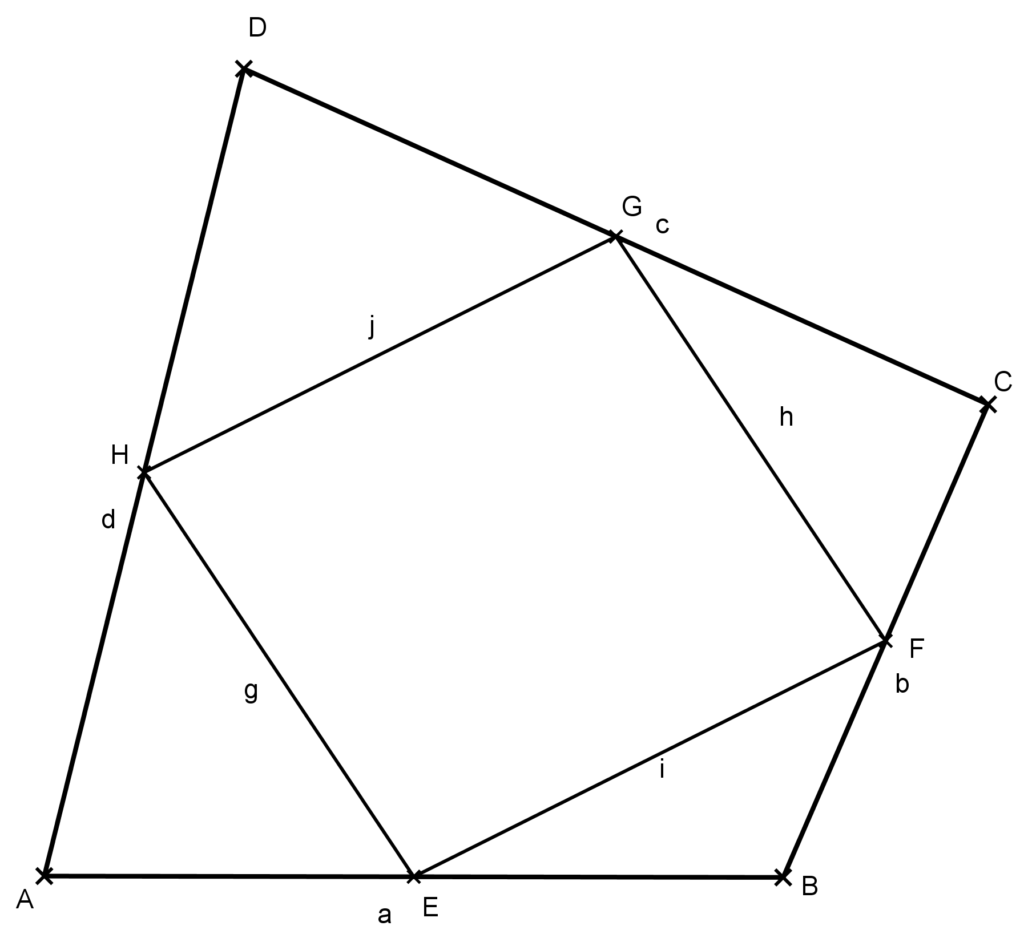
Az előző feladatban láttuk, hogy az EH szakasz az ABD háromszög középvonala, így az AEH háromszög területe az ABD háromszög területének a negyede. Hasonlóan a GFC háromszög területe a BCD háromszög területének a negyede. Mivel az ABD és BCD háromszög együtt megadja az ABCD négyszöget, így az AEH és FCG háromszögek területének összege az ABCD négyszög területének a negyede.

Hasonlóan látható be, hogy az EBF és HGD háromszögek területének az összege is az ABCD négyszög területének a negyede.

Ezzel beláttuk, hogy a négy háromszög területe együtt kiadja az ABCD területének a felét, tehát az EFGH területe is az ABCD négyszög területének a fele. Ezt érdemes végiggondolni konkáv négyszögre is, amit a tisztelt Olvasóra bízunk. Ezzel a feladatot megoldottuk.

***

Emelt szintű feladat vektorokkal

• 8. feladat: Bizonyítsuk be, hogy bármely paralelogrammában az oldalak négyzetösszege egyenlő az átlók négyzetösszegével! (Paralelogramma-tétel)

Megoldás: Ezt a tételt sokféleképpen bizonyíthatjuk. Mi most a vektorok skaláris szorzatát használjuk fel a bizonyításhoz. Ehhez vegyük fel az ABCD paralelogrammát és vektorizáljuk az oldalait és átlóit az ábrának megfelelően.

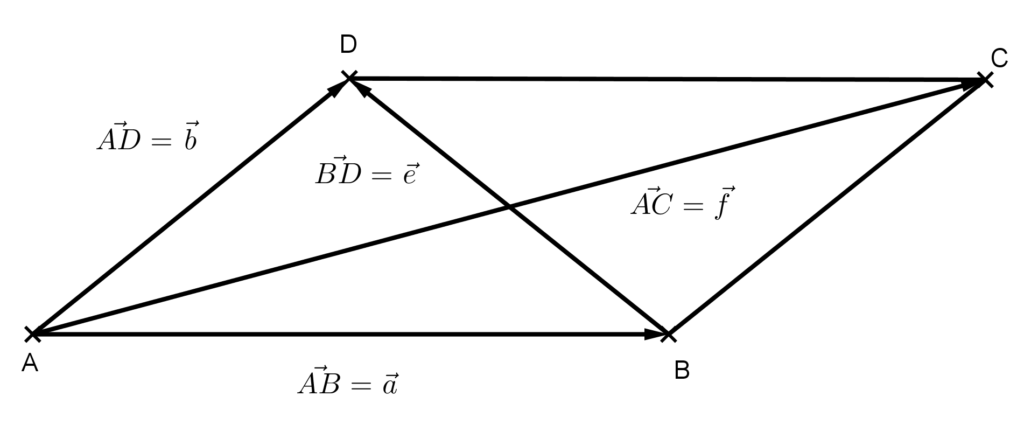
A vektorok közötti műveletek paralelogramma szabálya alapján

\overrightarrow{f}=\overrightarrow{a}+\overrightarrow{b} \text{ és } \overrightarrow{e}=\overrightarrow{b}-\overrightarrow{a}. 

A vektor abszolutértékét jelöljük a vektor betűjelének megfelelő kisbetűvel. Mivel egy vektor abszolutértékének négyzete egyenlő a vektor önmagával vett skaláris szorzatával, így

{{e}^{2}}+{{f}^{2}}={{\left( \overrightarrow{e} \right)}^{2}}+{{\left( \overrightarrow{f} \right)}^{2}}={{\left( \overrightarrow{b}-\overrightarrow{a} \right)}^{2}}+{{\left( \overrightarrow{a}+\overrightarrow{b} \right)}^{2}}. 

Végezzük el a négyzetre emeléseket és az összevonásokat:

{{\left( \overrightarrow{b}-\overrightarrow{a} \right)}^{2}}+{{\left( \overrightarrow{a}+\overrightarrow{b} \right)}^{2}}={{\left( \overrightarrow{b} \right)}^{2}}+{{\left( \overrightarrow{a} \right)}^{2}}-2\overrightarrow{b}\overrightarrow{a}+{{\left( \overrightarrow{a} \right)}^{2}}+{{\left( \overrightarrow{b} \right)}^{2}}+2\overrightarrow{a}\overrightarrow{b}=2{{a}^{2}}+2{{b}^{2}}.

Így

{{e}^{2}}+{{f}^{2}}=2{{a}^{2}}+2{{b}^{2}}. 

Ezzel a feladatot megoldottuk.

***

Emelt szintű feladat a háromszög súlyvonalára

Most alkalmazzuk az előző feladatot a háromszög súlyvonalai hosszának meghatározására. A háromszög súlyvonala a háromszög egy csúcsát a szemközti oldal felezőpontjával összekötő szakasz.

• 9. feladat: Fejezzük ki a háromszög súlyvonalainak a hosszát az oldalainak a hosszával.

Megoldás: Vegyük fel az ABC háromszög A csúcshoz tartozó súlyvonalát! Ezután tükrözzük a háromszöget az a oldalának felezőpontjára az ábra alapján.

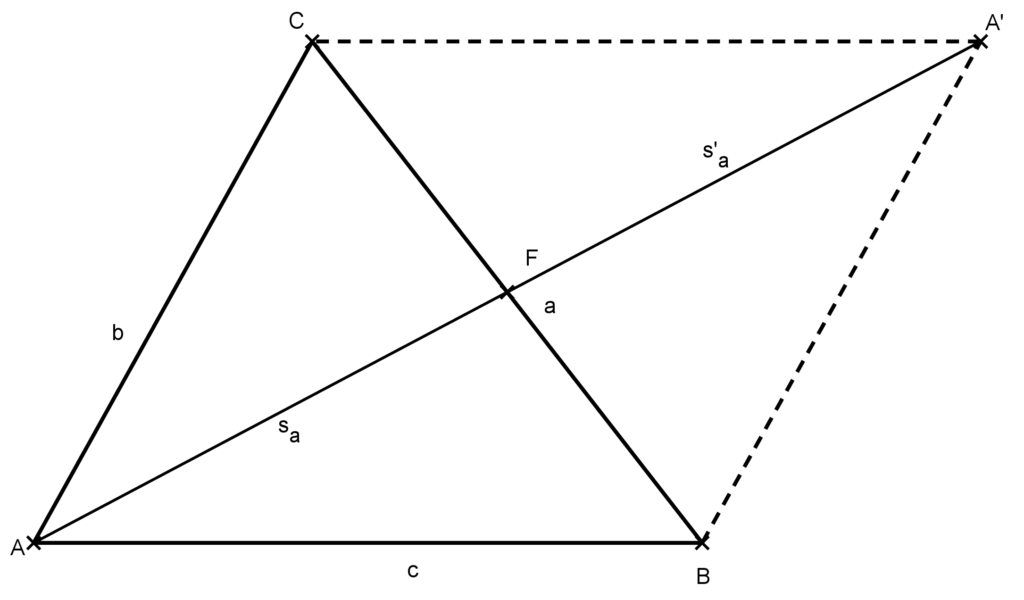
A tükrözés következtében létrejön az ABA’C paralelogramma. Alkalmazzuk erre a paralelogrammma-tételt.

Így

{{\left( 2{{s}_{a}} \right)}^{2}}+{{a}^{2}}=2{{b}^{2}}+2{{c}^{2}},

amiből kapjuk, hogy

{{s}_{a}}=\sqrt{\frac{2{{b}^{2}}+2{{c}^{2}}-{{a}^{2}}}{4}}. 

Hasonló összefüggés írható fel a többi súlyvonalra is. Ezzel a feladatot megoldottuk.

***

Emelt szintű feladat a paralelogramma területére

• 10.feladat: Legyen az ABCD paralelogramma két szomszédos oldalának hossza a és b, ahol b nem nagyobb a a-nál. Adjuk meg a paralelogramma szögfelezői által meghatározott négyszög és a paralelogramma területének az arányát!

Megoldás: Tudjuk, hogy a paralelogramma bármely két szomszédos szögének az összege 180°, így a szomszédos szögfelezők merőlegesek egymásra. Ez alapján az általuk meghatározott négyszög téglalap. Vegyük fel az alábbi ábrát.

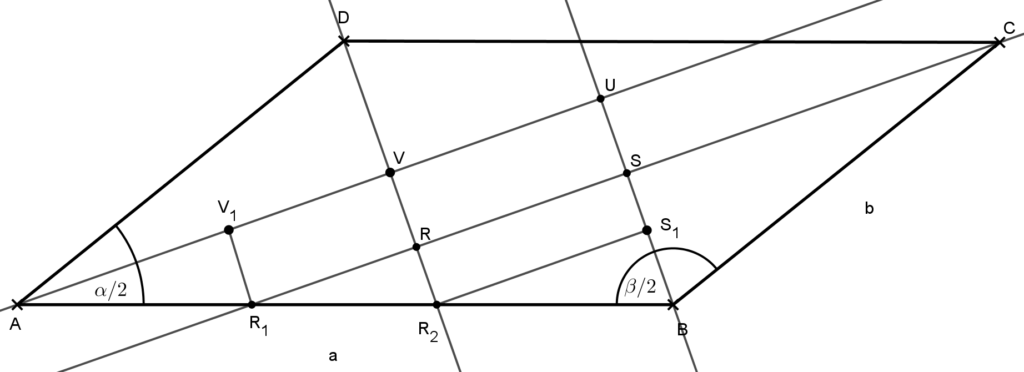
Metssze a C csúcsnál levő szögfelező az AB oldalt R₁, a D csúcsnál levő pedig R₂ pontban. A téglalap csúcsai legyenek R, S, U, V. A CR₁B háromszög egyenlőszárú, mert a B csúcsnál levő szögfelezője merőleges az R₁C oldalra. Emiatt az R₁B=b, így R₁A=a–b.

Hasonló okok miatt R₂B is a-b. Legyen R₁V₁ párhuzamos RV-vel és R₂S₁ párhuzamos RS-sel. Ekkor létrejön az AR₁V₁ és az R₂BS₁ derékszögű háromszög. Mindkettő átfogója a-b, a jelölt szögekkel szemközti befogójuk pedig egyenlő a téglalap egy-egy oldalával.

Felírhatjuk ezekben a derékszögű háromszögben, hogy

VR={{V}_{1}}{{R}_{1}}=(a-b)\cdot \sin \frac{\alpha }{2}, \text{ illetve } RS={{S}_{1}}{{R}_{2}}=(a-b)\cdot \sin \frac{\beta }{2}.

Mivel a két félszög összege 90°, ezért egymás pótszögei, így

\sin \frac{\beta }{2}=\cos \frac{\alpha }{2}.

Tehát

RS={{S}_{1}}{{R}_{2}}=(a-b)\cdot \cos \frac{\alpha }{2}.

Most már felírhatjuk a téglalap területét:

RS\cdot VR=\left ( a-b \right )^2\cdot \sin\frac{\alpha }{2}\cdot \cos\frac{\alpha }{2}=\frac{(a-b)^2}{2}\cdot \sin\alpha 

Itt felhasználtuk a kétszeres szög szinuszára vonatkozó addíciós tételt, ami alapján

\sin \frac{\alpha }{2}\cdot \cos \frac{\alpha }{2}=\frac{1}{2}\cdot 2\sin \frac{\alpha }{2}\cdot \cos \frac{\alpha }{2}=\frac{1}{2}\cdot \sin \left( 2\cdot \frac{\alpha }{2} \right)=\frac{1}{2}\cdot \sin \alpha.

Mivel a paralelogramma területe

T=a\cdot b\cdot \sin \alpha ,

így a két terület hányadosa

\frac{{{T}_{t}}}{T}=\frac{{{\left( a-b \right)}^{2}}\cdot \sin \alpha }{2ab\cdot \sin \alpha }=\frac{{{\left( a-b \right)}^{2}}}{2ab}.

Ezzel a feladatot megoldottuk.

***

Összefoglalás

A fenti összeállításban egymásra épülő, egyre nehezedő 10 feladaton keresztül mélítettük el a paralelogrammával kapcsolatos ismereteinket.

Szeretnél még több, hasonló cikket olvasni? Akkor böngéssz a blogunkon Matekos blog!

Emelt szintű érettségire készülsz, vagy elsőéves egyetemista vagy? Ekkor ajánljuk figyelmedbe az online tanuló felületünket és a felkészülést segítő csomagjainkat. Az ezekkel kapcsolatos részletekről itt ÉrettségiPro+ olvashatsz.

Összegyűjtöttük az eddigi összes emelt szintű matematika érettségi feladatsort és a megoldásokat. Ezt a gyűjteményt, valamint az érettségire készüléssel kapcsolatos hasznos tanácsokat a Emelt szintű matematika feladatsorok linken érheted el.

Szerző: Ábrahám Gábor (szakmai önéletrajz)

Cikkek

A szerző további cikkei megtalálhatók a Budapesti Fazekas Milyály Gyakorló Általános Iskola és Gimnázium matematika oktatási portálján:

• Feladatok megoldása az analízis eszközeivel.
• Függvény és inverze egyenletekben
• A háromszög területe
• Polinomalgebrai feladatok
• Szélsőértékfeladatok megoldása elemi úton

Az emelt szintű érettségire készüléssel kapcsolatos írásaink a 34 hét alatt új tudás születik, illetve 17 fejezet matematikából linken érhetők el.

A szerző által írt tankönyvek a Maxim Kiadó linken találhatók.

Matek versenyre készülőknek

Ha olyan ambícióid vannak, hogy szeretnél matematikával versenyzés szintjén foglalkozni, akkor javaslom az Erdős Pál Matematikai Tehetségondozó Iskolát. Ezzel vonatkozó részletek ezen linken Erdős Pál Matematikai Tehetséggondozó Iskola olvashatók. A matematika versenyek témáit feldolgozó könyvek, kiadványok (a szerző Egyenlőtlenségek I.-II. című könyvei is) a MATE alapítvány, kiadványok linken kersztül vásárolhatók meg.