A hétköznapi életben körbevesz minket a geometria, például a téglalap, mint speciális paralelogramma sűrűn előfordul környezetünkben.
Mint a geometria neve is jelzi, ez a tudomány a gyakorlati életből fejlődött ki, hisz a földmérés szülötte. Így nem meglepő, hogy az első nyomai Kr. e. 2000-ből Mezopotámiából és Egyiptomból származnak. Már akkor ismerték a derékszögű síkidomok területének, illetve az egyszerűbb testek térfogatának kiszámítását. Precíz tudománnyá válása az ókori görögök munkája nyomán indult el, ekkor jelent meg a dedukció (levezetés, bizonyítás) a matematikában, ami irányt szabott a geometria fejlődésének.
Ebben a cikkben egy nagyon fontos négyszög fajtával, a paralelogrammával foglalkozunk. Először megismerkedünk a paralelogramma definíciójával, majd bebizonyítjuk néhány tulajdonságát. Ezután levezetjük a kerület- illetve területképletét. Ha valaki szeretné elmélyíteni a cikkben található elméleti ismereteket, annak ajánljuk a Paralelogramma: feladatok egyszerűtől az emelt szintig című cikkünket. Ezt ITT lehet elérni.
Kinek hasznos az alábbi cikkünk?
Neked, ha általános iskolás vagy, és most ismerkedsz a négyszögfajtákkal.
Neked, ha érettségire készülsz, és nagyobb gyakorlatra szeretnél szert tenni geometriából.
Neked, ha esetleg már régebben voltál iskolás, ugyanakkor valamiért most szükséged lenne paralelogrammákkal kapcsolatos ismeretekre, és szeretnéd feleleveníteni azokat. Mi segítünk! Olvasd el cikkünket, és megtalálod a választ kérdéseidre.
A paralelogramma fogalma
A paralelogramma olyan négyszög, melynek szemközti oldalai párhuzamosak.
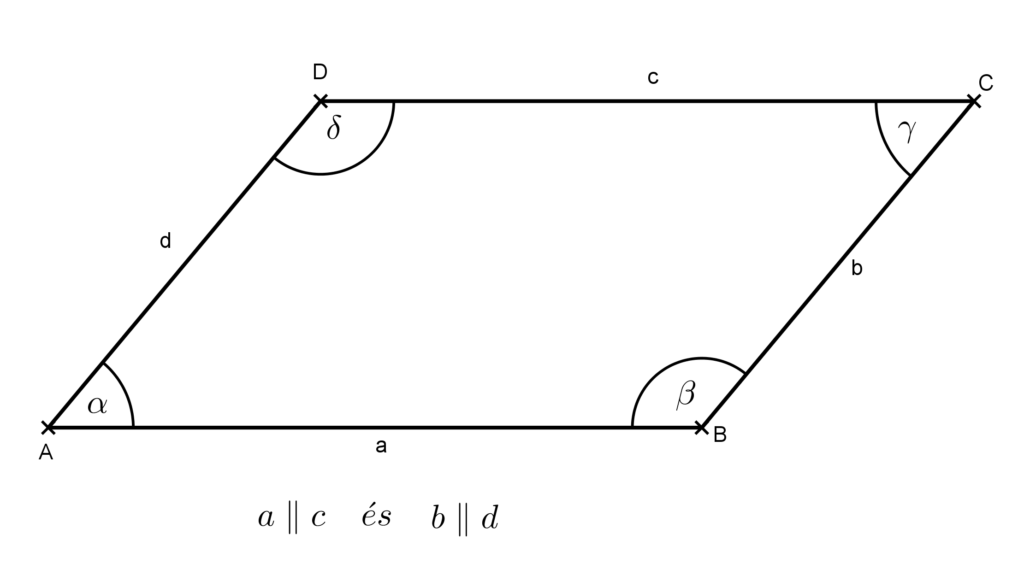
A paralelogramma tulajdonságai
Összefüggés a szögei között
- tulajdonság: A paralelogramma szemközti szögei egyenlők.
Bizonyítás: Mivel a szemközti oldalai párhuzamosak, ezért a szemközti szögei váltószögek, amiből következik, hogy egyenlők. Így
\alpha =\gamma \text { és } \beta =\delta .Ezt kellett bizonyítani.
A tétel megfordítása: Ha egy négyszögben két-két szemközti szög egyenlő, akkor a négyszög paralelogramma.
Bizonyítás: A feltétel szerint
\alpha =\gamma \text { és } \beta =\delta ,
így
2\alpha +2\beta =360{}^\circ.Ebből következik, hogy
\alpha +\beta =180{}^\circ , \text{ azaz } \beta =180{}^\circ -\alpha .Mivel az A és B csúcs esetén az AB oldal közös, így BC párhuzamos DA, illetve a B és C csúcs esetében a BC oldal közös, ezért AB párhuzamos CD. Így beláttuk, hogy az ABCD négyszög szemközti oldalai párhuzamosak, tehát teljesül rá a paralelogramma definíciója. Ezt kellett bizonyítani.
***
A következő állítás és megfordítása az előzőekben látott módon bizonyítható. ezt a tisztelt olvasóra bízzuk.
2. tulajdonság: A paralelogramma bármely két szomszédos szögének összege 180°
A tétel megfordítása: Ha egy négyszögben bármely két szomszédos szög összege 180°, akkor a négyszög paralelogramma.
***
Összefüggés az oldalai között
3. tulajdonság: A paralelogramma szemközti oldalainak a hossza egyenlő.
Bizonyítás: Vegyük fel az AC átlóját az ábrának megfelelően.
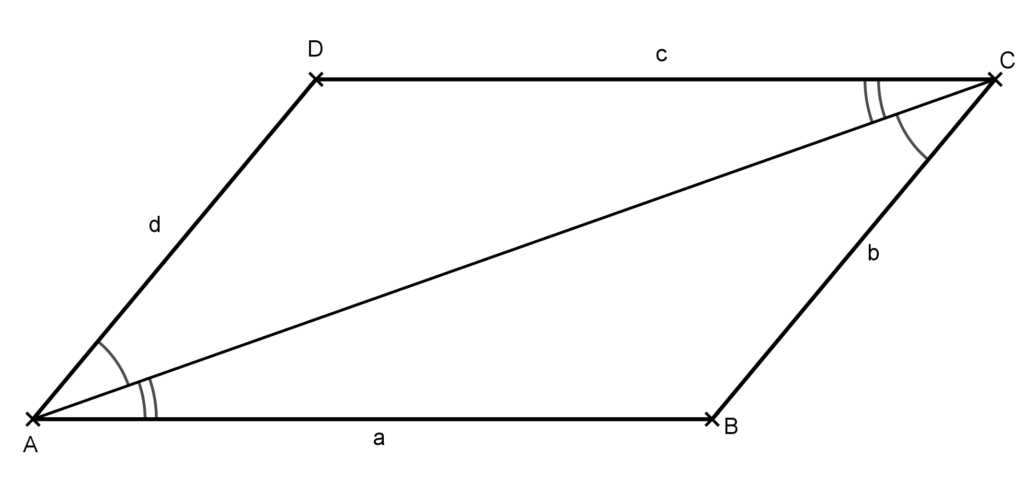
Ezzel a paralelogrammát felbontottuk az ABC és CDA háromszögekre. Ebben a két háromszögben közös az AC oldal, valamint egyenlők az ábrán egy, illetve két körívvel jelölt szögek, mivel váltószögek. Ebből következik, hogy az ABC és CDA háromszög egybevágó, így megfelelő oldalai egyenlők. Tehát AB=CD és BC=AD. Ezt kellett bizonyítani.
Az állítás megfordítása: Ha egy négyszög két-két szemközti oldala egyenlő, akkor a négyszög paralelogramma.
Bizonyítás: Legyen az ABCD négyszög olyan, amelyben AB=CD és BC=DA. Húzzuk be a négyszög AC átlóját. Ez a négyszöget az ABC és CDA háromszögekre bontja, melyekben az oldalak páronként egyenlők, így a két háromszög egybevágó.
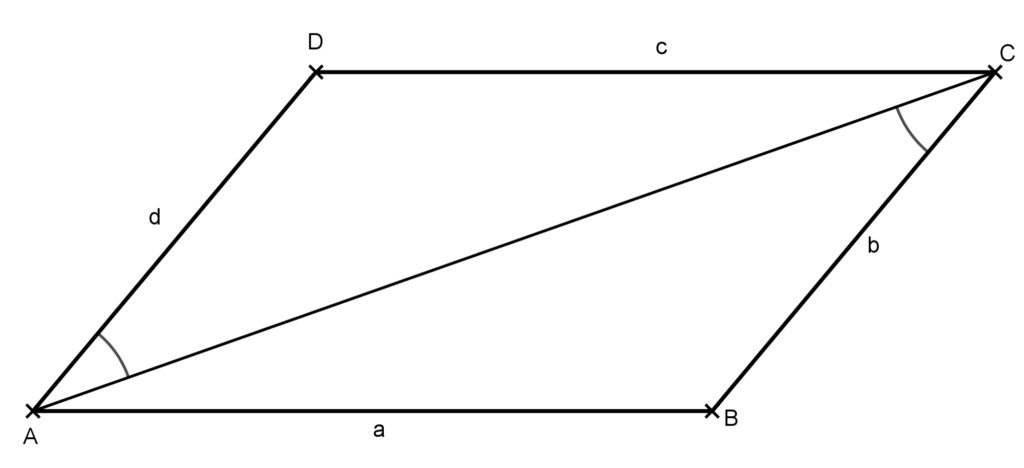
Az egybevágóságból következik, hogy az előző ábrán azonos módon jelölt szögek egyenlők, amiből jön, hogy BC párhuzamos AD-vel. Hasonlóan lehet belátni a másik két oldal párhuzamosságát is. Ezzel a tételt bizonyítottuk.
***
Az alábbi tulajdonság nyilvánvaló következménye az eddigieknek, ugyanakkor a tétel megfordítása nagyon fontos, mert sok esetben használhatjuk feladatok megoldásában.
4. tulajdonság: A paralelogramma két szemközti oldala párhuzamos és egyenlő.
Bizonyítás: Következik az eddigi tulajdonságokból.
A tétel megfordítása: Ha egy négyszög két oldala párhuzamos és egyenlő, akkor a négyszög paralelogramma.
Bizonyítás: Legyen az ABCD négyszögben az BC oldal párhuzamos és egyenlő a DA oldallal. Vegyük fel négyszög AC átlóját az ábrának megfelelően.
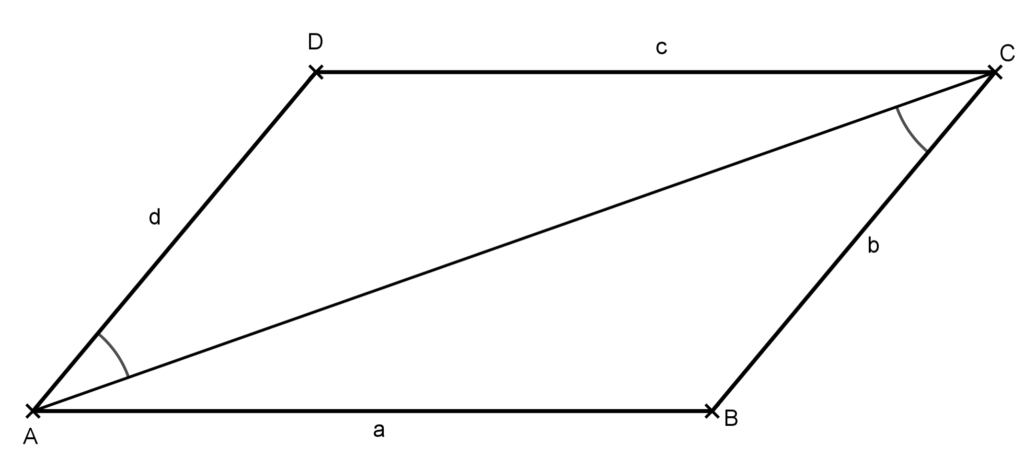
Mivel DA párhuzamos BC-vel, ezért DAC szög és az ACB szög váltószög, amiből következően egyenlők. A feltételek figyelembevételével kapjuk, hogy az ABC és ACD háromszögben egyenlő két-két oldal és az általuk bezárt szög, így a két háromszög egybevágó. Ebből következik, hogy AB=CD, így az ABCD négyszögben a szemközti oldalak egyenlők, azaz a négyszög paralelogramma. Ezt kellett bizonyítani.
***
Az átlói és szimmetriája
5. tulajdonság: A paralelogramma átlói felezik egymást.
Bizonyítás: Legyen az ABCD paralelogramma két átlójának metszéspontja az alábbi ábrának megfelelően M.
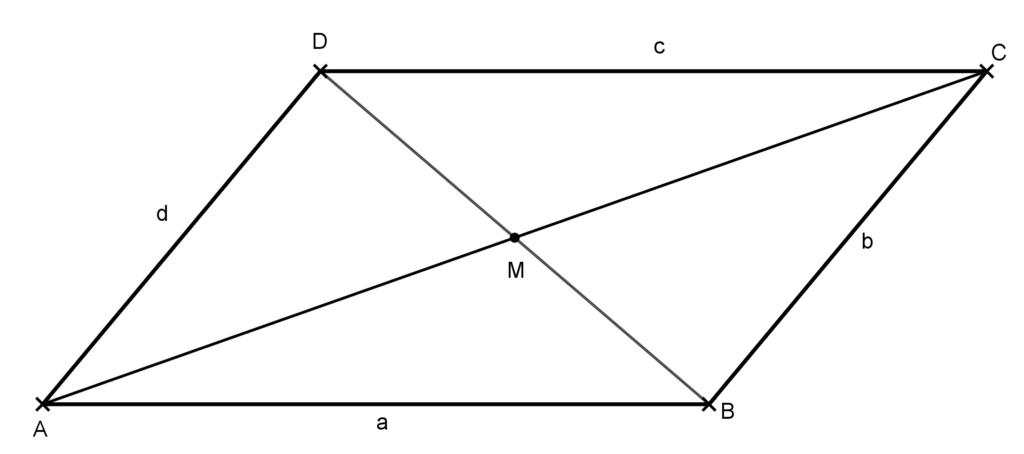
Mivel a szemközti oldalai egyenlők és párhuzamosak, ezért az ABM és a CDM háromszögben AB=CD, valamint a rajtuk fekvő szögek páronként váltószögek, tehát egyenlők. Így a két háromszög egybevágó, amiből következik, hogy AM=MC és BM=MD, azaz az átlói felezik egymást. Ezt kellett bizonyítani.
A tétel megfordítása: Ha egy négyszög átlói felezik egymást, akkor a négyszög paralelogramma.
Bizonyítás: Mivel az alábbi ABCD négyszög átlói felezik egymást, ezért AM=MC és BM=MD. Másrészt az M pontnál azonosan jelölt szögek csúcsszögek, tehát egyenlők. Lásd az ábrát.
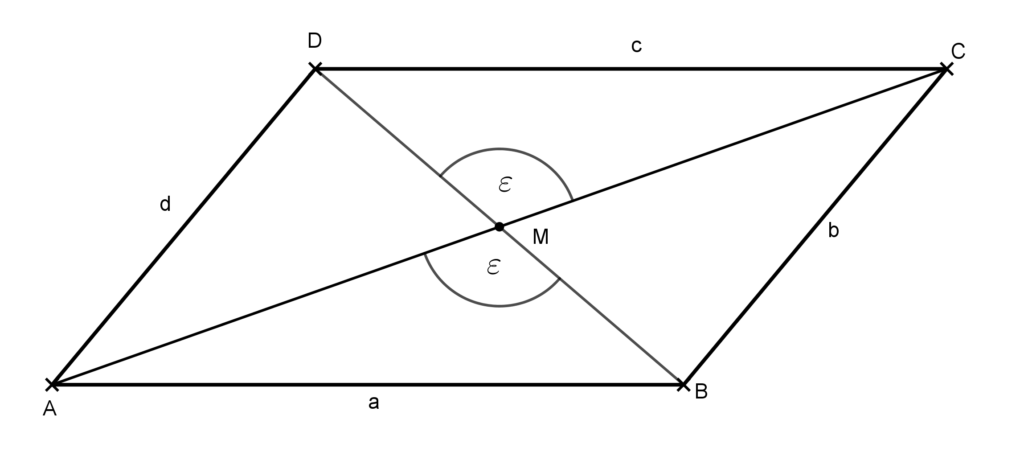
Így az ABM és CDM háromszögben két-két oldal és az általuk bezárt szög egyenlő, amiből következik, hogy a két háromszög egybevágó. Ez pedig maga után vonja, hogy AB=CD. Hasonlóan igazolható, BC=DA. Tehát az ABCD négyszög paralelogramma, amit bizonyítani akartunk.
***
Az előző tételekből következik az alábbi két tétel.
6. tulajdonság: A paralelogramma középpontosan szimmetrikus négyszög.
Az állítás megfordítása: Ha egy négyszög középpontosan szimmetrikus, akkor paralelogramma.
***
Foglaljuk össze az eddigieket
Az előbbi tárgyalt tételek és megfordításaik alapján több egymással egyenértékű definíciót is megfogalmazhatunk a paralelogrammára. Az alábbiak bármelyike használható a paralelogramma definíciójaként, a többi tulajdonság pedig abból következik.
Az a négyszög paralelogramma, amelynek
- szemközti oldalai párhuzamosak;
- szemközti oldalai egyenlők;
- szemközti szögei egyenlő nagyságúak;
- bármely két szomszédos szögének összege 180°;
- két szemközti oldala egyenlő és párhuzamos;
- átlói felezik egymást;
- középpontosan szimmetrikus.
***
A középvonalai
Mi a négyszög középvonala? Milyen speciális tulajdonsággal rendelkezik a paralelogramma középvonala?
A négyszög középvonalainak a szemközti oldalainak felezőpontjait összekötő szakaszokat nevezzük. Minden négyszögnek két középvonala van.
Tétel: A paralelogramma két oldalának felezőpontját összekötő középvonala párhuzamos és egyenlő a másik két oldallal.
Bizonyítás: Legyen adott az ABCD paralelogramma, melynek egyik középvonala az ábrának megfelelően az AB oldal E felezőpontját a CD oldal F felezőpontjával összekötő szakasz.
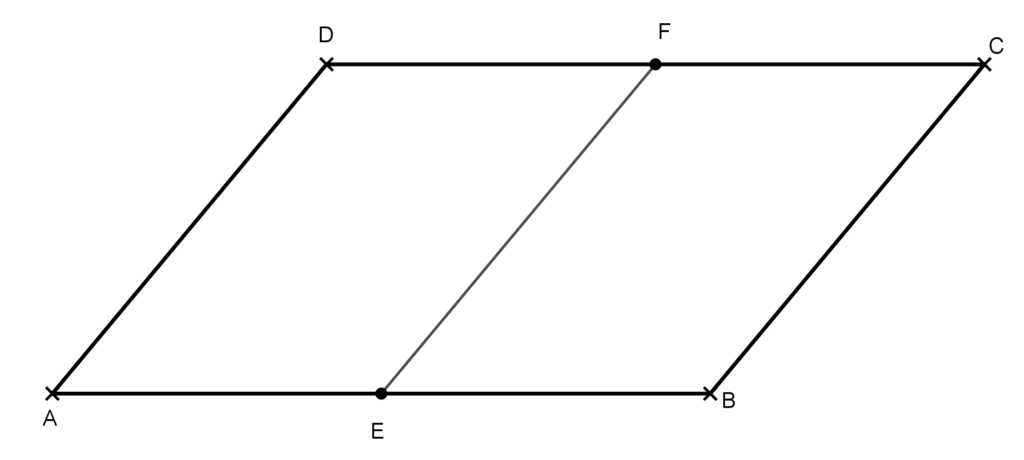
Ezzel az eredeti paralelogrammát két négyszögre bontjuk. Tekintsük közülük az AEFD négyszöget. Mivel az ABCD négyszög paralelogramma, ezért AB párhuzamos és egyenlő CD-vel. Emiatt AE párhuzamos és egyenlő FD-vel. Ezért a 4. tulajdonság megfordítása alapján az AEFD négyszög paralelogramma, azaz EF párhuzamos és egyenlő AD-vel. Ezt kellett bizonyítani.
***
A kerülete
A paralelogramma kerületét könnyen meghatározhatjuk, ha felhasználjuk azt a tulajdonságát, hogy szemközti oldalainak a hossza egyenlő.
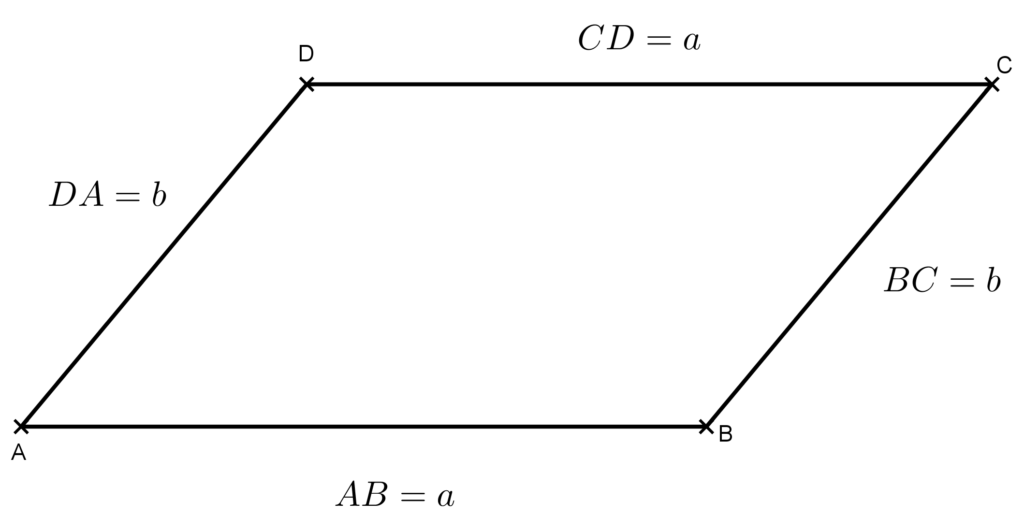
Legyen az ABCD paralelogramma két szomszédos oldalának a hossza az ábrának megfelelően AB=a,illetve BC=b. Ekkor a kerülete
K=AB+BC+CD+DA=2a+2b=2(a+b)
***
A paralelogramma területe
A területének meghatározása előtt bebizonyítunk egy fontos tételt.
Tétel: Ha két paralelogramma egy-egy oldala és ezen oldalakhoz tartozó magasságuk egyenlő, akkor a területük is egyenlő.
Bizonyítás: A bizonyítás az alábbi videón látható.
***
Ezek után már könnyen megadhatjuk a területképletét felhasználva, hogy ha egy téglalap két szomszédos oldalának a hossza a és b, akkor a területe
T=a\cdot b
Tétel: Ha egy paralelogramma egyik oldalának a hossza a, a hozzá tartozó magasságának a hossza m, akkor a területe
T=a\cdot m.
Bizonyítás: Vegyük fel az ABCD paralelogrammát és az A’B’C’D’ téglalapot, melyre teljesül, hogy a=AB=A’B’ és B’C’=m, ahol m az AB oldalhoz tartozó magassága. Lásd az ábrát.
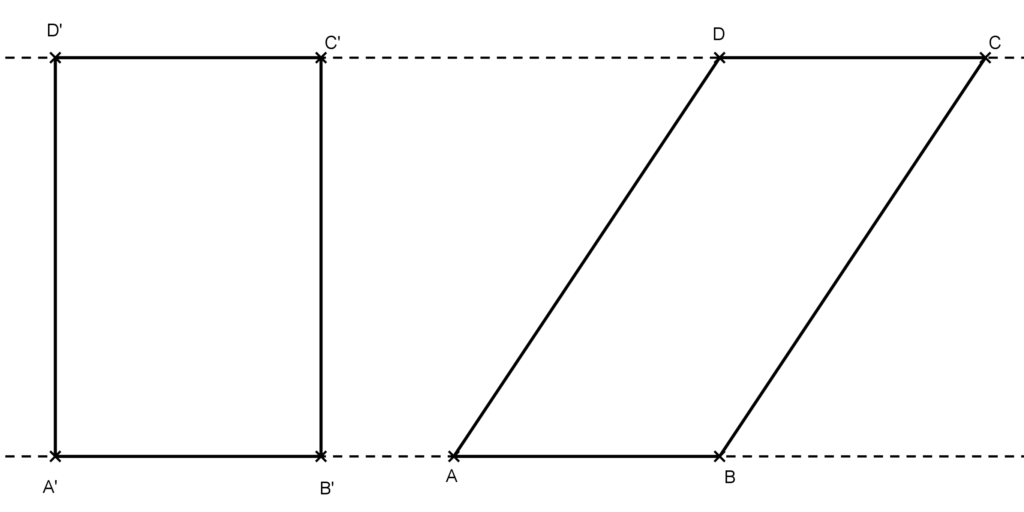
Mivel a téglalap speciális paralelogramma, ezért az előző tétel alapján a két négyszög területe egyenlő. Tehát
T=A'B'\cdot B'C'=AB\cdot m=a\cdot m.
Ezzel a tételt bizonyítottuk.
***
A paralelogramma területét kiszámolhatjuk két oldalának és az általuk bezárt szögnek az ismeretében is. A bizonyítás könnyen levezethető trigonometrikus ismeretekkel.
Tétel: Ha egy paralelogramma két szomszédos oldalának a hossza a és b, valamint az általuk bezárt szög α, akkor a területe
T=a\cdot b\cdot \sin \alpha .
***
Összefoglalás
A fenti összeállításban szerepelt a paralelogramma fogalma, szó volt az egymással ekvivalens tulajdonságairól, amik közül bármelyiket használhatjuk definícióként. Levezettük a kerületére és területére vonatkozó képletet.
Szeretnéd alkalmazni az itt látottakat, akkor ajánljuk figyelmedbe a Paralelogramma: feladatok egyszerűtől az emelt szintig című cikkünket, melyet ITT olvashatsz.
Ha szeretnél további matematikai témájú cikkeket olvasni, akkor látogasd meg a Matekos blog című oldalunkat. Ezt ITT érheted el.
Emelt szintű érettségire készülsz, vagy elsőéves egyetemista vagy? Ekkor ajánljuk figyelmedbe az online tanuló felületünket és a felkészülést segítő csomagjainkat. Az ezekkel kapcsolatos részletekről itt ÉrettségiPro+ olvashatsz.
Összegyűjtöttük az eddigi összes emelt szintű matematika érettségi feladatsort és a megoldásokat. Ezt a gyűjteményt, valamint az érettségire készüléssel kapcsolatos hasznos tanácsokat a Emelt szintű matematika feladatsorok linken érheted el.
Látogasd meg youtube csatornánkat, ahol emelt szintű feladatok megoldásával, illetve tételek bizonyításával kapcsolatos videók közül válogathatsz. A videócsatornát ITT érheted el. Feldolgoztuk a teljes emelt szintű analízis tananyagot.
Szerző: Ábrahám Gábor (szakmai önéletrajz)

