A Pitagorasz-tétel az a geometriai ismeret, ami leginkább megmaradt mindenki számára az általános, illetve középiskolai tanulmányokból. Ebből is látszik, hogy fontos a geometria területén betöltött szerepe. Szinte minden témakörben előkerül alkalmazás szintjén. Jelentőségét misem jelzi jobban, mint hogy négyszáznál is több bizonyítása ismert.
Az alábbi cikkben megfogalmazzuk és bizonyítjuk a Pitagorasz-tételt és annak megfordítását. Megismerkedünk a pitagoraszi számhármasokkal és azok előállítási módjával. Végül az alapoktól az emelt szintű matematika érettségi feladatokig kilenc problémán keresztül alkalmazzuk az elméleti ismereteket.
A feladatok egymásra épülnek, így lehetőséget nyújtanak arra, hogy azok is könnyen fel tudják eleveníteni a Pitagorasz-tétellel kapcsolatos ismereteiket, akik már régen foglalkoztak geometriával.
Ezt az elvet követtem az ÉrettségiPro+ emelt szintű érettségire felkészítő tananyagának összeállításánál is. Ott külön fejezetben foglalkozunk Pitagorasz tételével. Ezzel kapcsolatosan további részletek az ezen a linken találhatók.
Kinek hasznos az alábbi cikkünk?
Neked, ha érettségire készülsz, és át szeretnéd ismételni a Pitagorasz-tétellel kapcsolatos ismereteidet és rutint szeretnél szerezni a vele kapcsolatos feladatok megoldásában. Ehhez nyújt még segítséget az ÉrettségiPro+ tananyaga is, melyhez információkat ITT találsz.
Neked, ha csak szeretnél jártasságot szerezni a Pitagorasz-tétellel kapcsolatos feladatok megoldása terén.
Neked, ha esetleg már régebben voltál iskolás, ugyanakkor valamiért most szükséged lenne Pitagorasz tételével kapcsolatos ismeretekre, és szeretnéd feleleveníteni azokat.
Mi segítünk! Olvasd el cikkünket, és megtalálod a választ kérdéseidre.
Pitagorasz és a pitagoraszi iskola

Pitagorasz az ókori görög matematika egyik legnagyobb alakja volt, aki időszámításunk előtti IV. században élt. Legendákkal övezett életéről nem tudunk túl sokat. Szamosz szigetéről származik, tanult Egyiptomban és járt Babilóniában. Valószínűleg széles látókörű, természettudományokkal és matematikával elmélyülten foglalkozó, valamint a filozófia iránt is érdeklődő tudós volt.
Pitagorasz a dél-itáliai Kroton városában iskolát alapított, melyben az aritmetikából önálló területként kivált a számelmélet. A természet, a társadalom örök törvényeit kutatták, melyeket a matematika, a csillagászat és a zene tanulmányozásával igyekeztek megtalálni. A zenei összhangban mutatkozó számszerű szabályosságok sugallták számukra azt a gondolatot, hogy az élet különböző területein fennálló harmóniát az egész számok biztosítják. Ezért is foglalkoztak behatóan a természetes számokkal, ami fontos szerepet játszott a számelmélet kialakulásában.
Megvizsgálták a természetes számok oszthatóságának kérdéseit, bevezették a számtani, a mértani és harmonikus arányokat.
Az általunk ismert Pitagorasz-tétel nem Pitagorasztól származik, hisz már előtte alkalmazták az ókori Egyiptomban, illetve Babilóniában. Ugyanakkor a pitegoreusok bizonyítást adtak rá, illetve megtalálták a “pitagoraszi számhármasok” végtelen sorát előállító módszert. Mellyel mi is foglalkozunk majd jelen írásunkban.
***
Pitagorasz-tétel és annak megfordítása
Pitagorasz-tétel
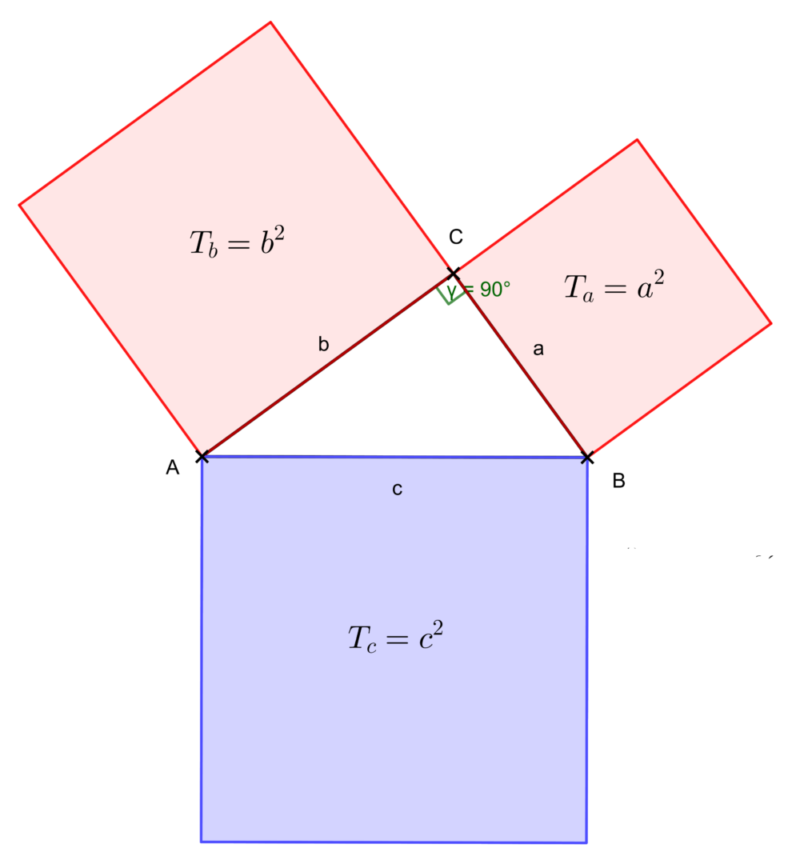
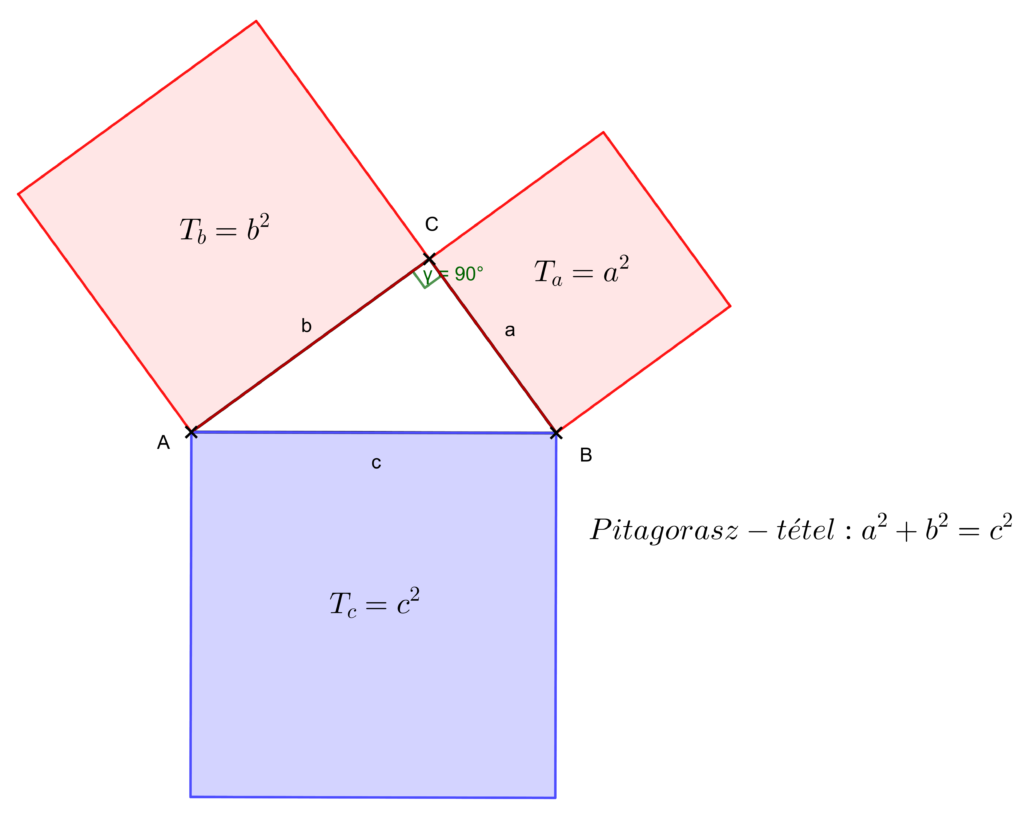
Tétel: Bármely derékszögű háromszögben a két befogóra rajzolt négyzetek területének összege egyenlő az átfogóra rajzolt négyzet területével.
A tételt az alábbi módon is megfogalmazhatjuk
Tétel: Bármely derékszögű háromszögben a két befogó hossszának négyzetösszege egyenlő az átfogó hosszának négyzetével.
A tétel bizonyítását lásd az alábbi videóban.
***
Pitagorasz-tétel megfordítása
Tétel: Ha egy háromszög háromszög a, b és c hosszúságú oldalaira fennáll az
a^2+b^2=c^2
összefüggés, akkor a háromszög derékszögű és átfogója a c oldal.
A Pitagorasz-tétel és megfordítása bizonyítását lásd az alábbi videóban.
***
Pitagoraszi számhármasok
Definíciók
Azt már általános iskolai tanulmányainkból tudjuk, hogy léteznek olyan derékszögű háromszögek, melyeknek, pl. centiméterben mérve, mindhárom oldala egész szám. Ilyen példul az a derékszögű háromszög melynek két befogója 3 cm és 4 cm, átfogója 5 cm. Könnyen végig gondolhatjuk, hogy ebből a háromszögből kiindulva előállíthatunk végtelen sok olyan derékszögű háromszöget, melyeknek mindhárom oldala centiméterben mérve egész szám, hisz vegyük a 3n, 4n centiméter hosszúságú befogókkal rendelkező derékszögű háromzöget, ahol n pozitív egész szám.
Ekkor
(3n)^2+(4n)^2=9n^2+16n^2=25n^2=(5n)^2,
Azaz a háromszög harmadik oldala 5n cm hosszú. A 3, 4 és 5 pitagoraszi számhármas, akárcsak a belőlük képezet 3n, 4n és 5n, ahol n pozitív egész szám.
Általánosan az
x^2+y^2=z^2
pitagoraszi egyenlet pozitív egész megoldásait pitagoraszi számhármasoknak nevezzük.
Kézenfekvő a kérdés, hogy az alfejezet első két bekezdésében megadott számokon kívül léteznek-e még pitagoraszi számhármasok?
Erre a kérdésre adunk választ ebben az alfejezetben.
A pitagoraszi egyenlet azon x, y, z pozitív egész megoldásait, melyekre teljesül, hogy legnagyobb közös osztójuk 1, azaz relatív prímek, primitív pitagoraszi számhármasoknak, vagy alapmegoldásoknak nevezzük. Ilyen pl. a 3, 4, 5, ugyanakkor nem alapmegoldás a 6, 8, 10, mert ezek legnagyobb közös osztója 2.
Az alapmegoldásokból előállíthatjuk a pitagoraszi egyenlet összes pozitív egész megoldását úgy, ahogy ezt a 3, 4 és 5 számokkal kapcsolatban láttuk az első két bekezdésben.
A piatgoraszi számhármasok előállítása
Az alábbi tétel a pitagoraszi egyenlet alapmegoldásainak előállításáról szól.
Tétel: Az
x^2+y^2=z^2
egyenlet alapmegoldásait a következő képlet szolgáltatja:
x=2mn, \text{ } y=m^2-n^2 \text{ } \text{ és } \text{ } z=m^2+n^2,ahol az m és n paraméterek melyekre teljesül, hogy különböző paritásúak, m>n és legnagyobb közös osztójuk 1.
A tétel bizonyításával most nem foglalkozunk, mert az meghaladja a jelen írás kereteit. Ha érdekel a bizonyítás, akkor megtalálod többek között Freud Róbert-Gyarmati Edit: Számelmélet című könyvének 286. oldalán.
Bizonyítás helyett megadunk inkább néhány pitagoraszi számhármast.
| m | n | x | y | z |
| 2 | 1 | 4 | 3 | 5 |
| 3 | 2 | 12 | 5 | 13 |
| 4 | 1 | 8 | 15 | 17 |
| 4 | 3 | 24 | 7 | 25 |
| 5 | 2 | 20 | 21 | 29 |
***
Pitagorasz-tétel alkalmazása
Alapfeladatok
Síkgeometria és a Pitagorasz-tétel
- 1. feladat: Egy 2,6 m hosszú létrát a függőleges falhoz támasztunk úgy, hogy a létra alja a fal aljától 1 méter távolságra helyezkedik el. Milyen magasan lesz a padlótól a létra teteje?
Megoldás: Készítsünk ábrát!
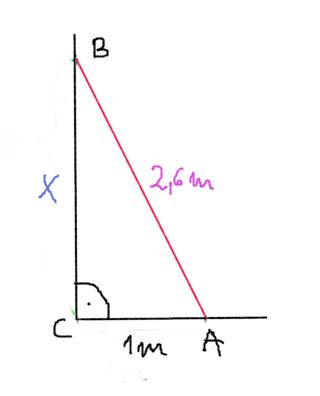
Az ABC derékszögű háromszögben adott az AB átfogó, ami 2,6 m és a CA befogó, ami 1 m. A feladat szerint a BC befogó hossza a kérdés.
Pitagorasz-tétel alapján:
x^2+1^2=2,6^2,
így
x^2=2,6^2-1^2=5,76.
Ebből kapjuk, hogy x=2,4.
Tehát a létra teteje a padlótól 2,4 méter távolságra van.
***
- 2. feladat: Egy ház padlásterének keresztmetszete egyenlő szárú háromszög, melynek alapja 10 m és szárai 6,5 méter hossszúak. Milyen magas a padlástér?
Megoldás: Készítsünk ábrát!
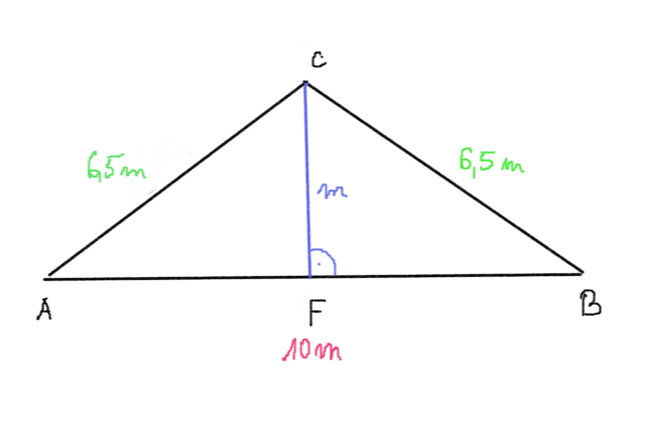
Az ABC egyenlő szárú háromszög alaphoz tartozó FC=m magasságát kérdezi a feladat. Az F pont felezi a háromszög AB alapját, így AF=5 m.
Írjuk fel az AFC derékszögű háromszögre Pitagorasz tételét:
AF^2+FC^2=AC^2,
azaz
5^2+m^2=6,5^2,
ahonnan
m^2=6,5^2-5^2=17,25.
Ebből m=4,15 két tizedes jegyre kerekítve.
Tehát a padlástér magassága 4,15 méter.
***
Térgeometria és a Pitagorasz-tétel
- 3. feladat (2006. október középszintű érettségi, 7. feladat) Egy négyzetes oszlop egy csúcsból kiinduló három élének hossza: a, a és b. Fejezze ki ezekkel az adatokkal az ebből a csúcsból kiinduló testátló hosszát!
Megoldás: Készítsünk ábrát
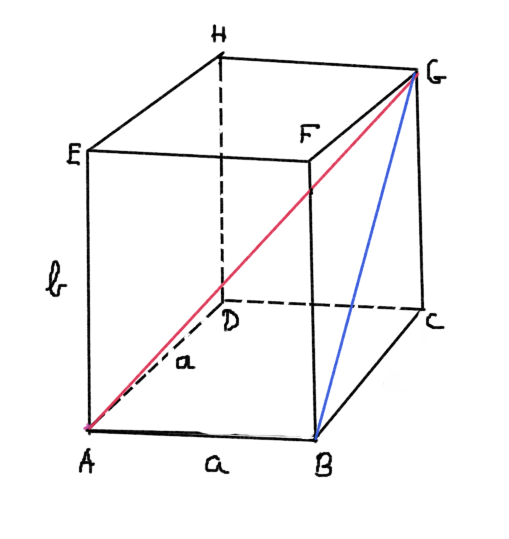
A feladat az AG testátlót kérdezi, miközben AB=a, AD=a és AE=b. Az AG hosszát az ABG derékszögű háromszögből számolhatjuk. Pitagorasz-tétel alapján:
AG^2=AB^2+BG^2=a^2+BG^2.
Még ki kell fejezni a BG lapátlót a-val és b-vel. Ezt a BCG derékszögű háromszögből tehetjük meg Pitagorasz-tétel felhasználásával:
BG^2=a^2+b^2.
Így
AG^2=a^2+BG^2=a^2+a^2+b^2=2a^2+b^2,
ahonnan
AG=\sqrt{2a^2+b^2}.Ezzel a feladatot megoldottuk.
***
Pitagorasz-tétel a középszintű feladatokban
Síkgeometriai feladatok
Trapéz
- 4. feladat: Egy árvízvédelmi gát keresztmetszete húrtrapéz alakú. A gát ferde oldala 4,1 méter hosszú és magassága 4 méter. A gát ferde oldalának közepén 4,5 méter hosszú vízszintes alagutat fúrnak és azt kiöntik betonnal. Mekkora a gát tetejének, illetve az aljának a szélessége?
Megoldás: Készítsünk ábrát a keresztmetszetről!
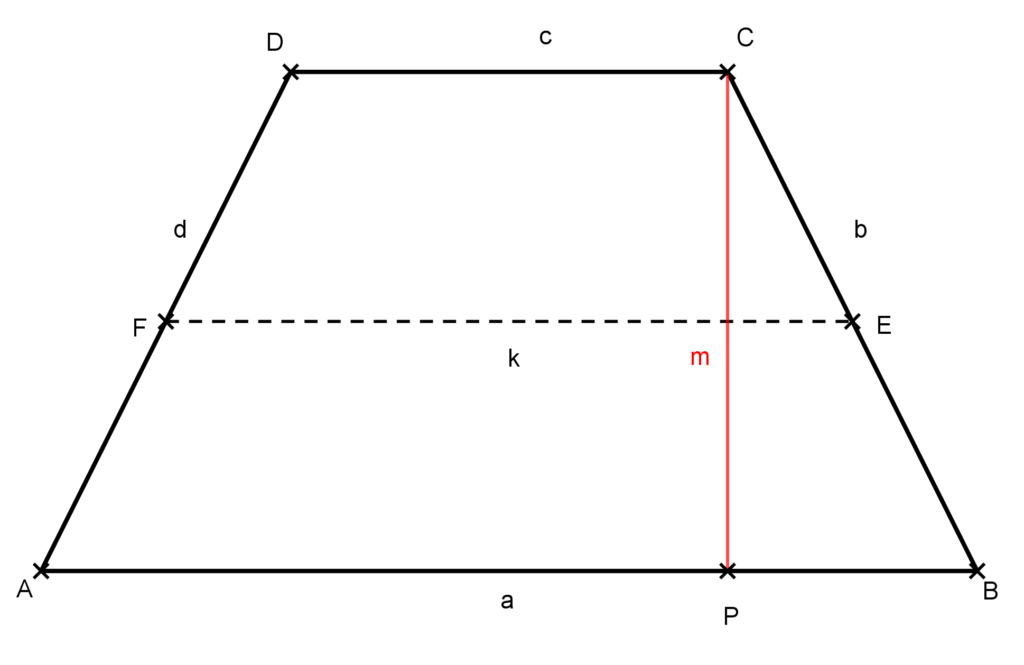
A feladat szerinti adatok a következők: m=4 méter, b=d=4,1 méter és k=4,5 méter. A k a trapéz középvonala, melyről tudjuk, hogy az alapok számtani közepe. Ezt bizonyítjuk is a trapézokról szóló cikkünkben, amely a Trapéz linken érhető el.
Tehát
k=\frac{a+c}{2},azaz
4,5=\frac{a+c}{2},így
a+c=9.
Ahogy a trapézokról szóló cikkünk 4. feladatában is írtuk a a magasság által levágott PB szakasz
PB=\frac{a-c}{2}.Tehát ha kiszámoljuk a PB szakasz hosszát, akkor a két alap összegére, illetve különbségére felírt a összefüggésből ki tudjuk számolni az a és c oldal hosszát.
A PB hosszának meghatározásához írjuk fel Pitagorasz tételét a PBC derékszögű háromszögben:
b^2=m^2+PB^2,
így
4,1^2=4^2+PB^2,
ahonnan
PB^2=4,1^2-4^2=0,81.
Így PB=0,9 méter, amiből következik, hogy a-c=1,8
Így az
\left\{\begin{matrix}
a+c=9 \\ a-c=1,8
\end{matrix}\right.egyenletrendszert kell megoldani.
Adjuk össze a két egyenletet, így kapjuk, hogy
2a=10,8,
azaz a=5,4 méter. Ebből könnyen jön, hogy c=3,6 méter.
Tehát a gát aljának a szélessége 5,4 méter, míg a teteje 3,6 méter széles.
***
Külső pontból körhöz húzott érintők
- 5. feladat: Egy kör K középpontjától 34 cm távolságra levő P pontból érintőket húzunk a körhöz. Mekkora az érintési pontok távolsága, ha az érintőszakaszok hossza 30 cm?
Megoldás: A szokásoknak megfelelően először készítsünk ábrát!
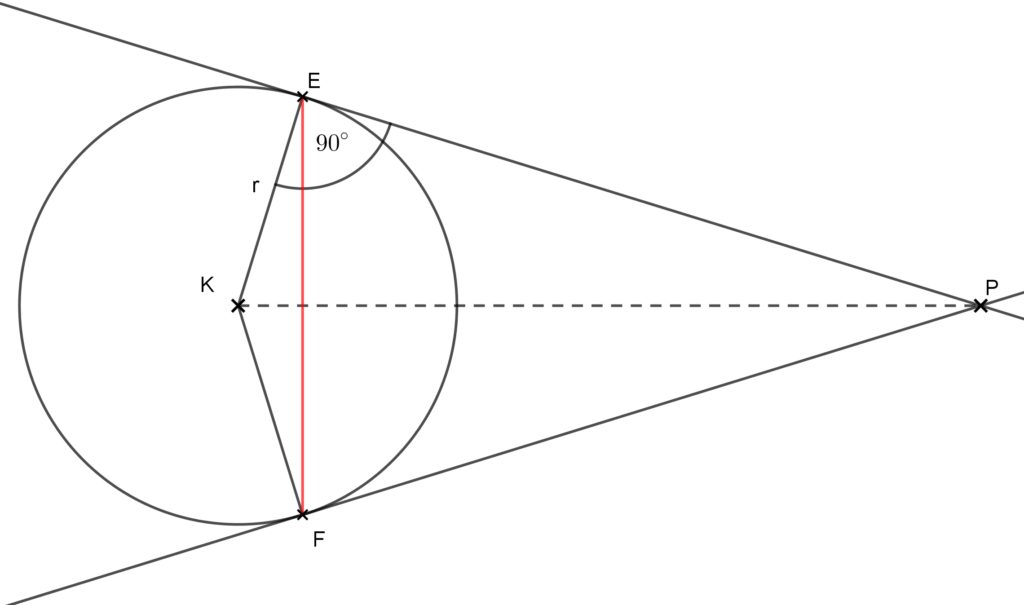
A feladat szerint PK=34 cm és PE=30 cm. Cél az EF szakasz hosszának meghatározása.
Mivel az FPEK négyszög két-két szomszédos oldala egyenlő, így ez a négyszög deltoid. Azt már bizonyítottuk a deltoidokról szóló cikkünkben (lásd Deltoid-fogalma, tulajdonságai, feladatok ), hogy a deltoid területe egyenlő az átlói szorzatának a felével. Így ha ki tudjuk számolni a feladatban szereplő deltoid területét valamilyen más módon, akkor az említett összefüggésből megkapjuk az EF szakasz hosszát.
Mivel az érintési pontba húzott sugár merőleges az érintőre, ezért az FPEK deltoid E-nél, illetve F-nél levő szöge derékszög, így felbontható két egybevágó derékszögű háromszögre. Ebből kiderül, hogy a területe egyenlő egy ilyen háromszög területének a kétszeresével. Mivel a derékszögű háromszög területe egyenlő két befogója szorzatának a felével, ezért elég a KE=r szakasz hosszát kiszámolni.
Ezt a Pitagorasz-tétel felírásával tehetjük meg:
r^2+PE^2=PK^2,
ahonnan
r^2=PK^2-PE^2=34^2-30^2=256.
Így r=16 cm.
A deltoid területére felírhatjuk, hogy
T=2\cdot\frac{r\cdot EP}{2}=\frac{EF\cdot PK}{2},így
EF=\frac{2r\cdot EP}{PK}=\frac{2\cdot16\cdot 30}{34}=\frac{480}{17} \text{ cm }.Tehát az érintési pontok távolsága 480/17 cm. Ezzel a feladatot megoldottuk.
***
Téregometriai feladat
- 6. feladat: (2007. május középszintű érettségi 15. feladat) Egy gyertyagyárban sokféle színű, formájú és méretű gyertyát készítenek. A folyékony, felhevített viaszt különféle formákba öntik. Az öntőhelyek egyikén négyzet alapú egyenes gúlát öntenek, melynek alapéle 5 cm, oldaléle 8 cm hosszú.
- a) Számítsa ki ennek a gúla alakú gyertyának a térfogatát! (Az eredményt cm3-ben, egészre kerekítve adja meg!)
- Ezen az öntőhelyen az egyik műszakban 130 darab ilyen gyertyát gyártanak.
- b) Hány liter viaszra van szükség, ha tudjuk, hogy a felhasznált anyag 6 %-a veszteség? (Az eredményt egy tizedes jegyre kerekítve adja meg!)
- A gúla alakú gyertyákat egyenként díszdobozba csomagolják.
- c) Hány cm2 papír szükséges 40 darab díszdoboz elkészítéséhez, ha egy doboz papírszükséglete a gúla felszínének 136%-a?
Megoldás: Készítsünk ábrát!
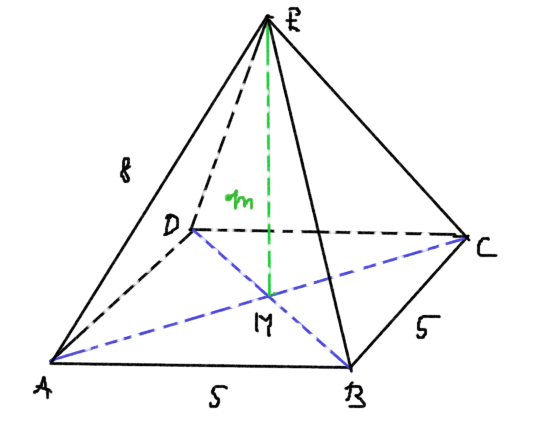
A feladat a) része
a) A gúla térfogata egyenlő az alapterülete és magassága szorzatának a harmadával. Így szükség van a test m magasságának a hosszára. Ezt az ábrán látható AME derékszögű háromszögből számolhatjuk ki.
A háromszög átfogja ismert, így az AM befogóját kell kiszámolnunk. Ez a szakasz a négyzet átlójának a fele és egyben az ABC egyenlőszárú derékszögű háromszög átfogójának a felével is egynelő. Így a Pitaggorasz-tételt használva kapjuk, hogy
(2AM)^2=AB^2+BC^2=5^2+5^2=50,
ahonnan
AM=\frac{\sqrt{50}}{2}=\frac{5\cdot\sqrt{2}}{2}\text{ cm }.Alkalmazzuk Pitagorasz tételét az AME háromszögben:
m^2=EA^2-AM^2=64-\left(\frac{5\cdot\sqrt{2}}{2}\right)^2=51,5.Ebből m=7,18 cm.
A gúla térfogata
V=\frac{a^2\cdot m}{3}=\frac{5^2\cdot 7,18}{3}=59,84 \text{ }cm^2.Így térfogat egészre kerekített értéke
V=60 \text{ }cm^3.A feladat b) része
b) A b) és c) rész megoldásához a százalékszámítással kapcsolatos cikkünket ajánljuk azok figyelmébe, akik úgy érzik, hogy ezen a téren vannak még hiányosságaik. A cikk a Százalékszámítás linken érhető el.
A feladat szerint 130 gyertyát szeretnének kiönteni. Ezek össztérfogata 7800 cm3. A feltételekből kiderül, hogy a vásárolt viasz 6%-át számítják veszteségnek, tehát a 7800 cm3 ennek a 94%-a.
Így a vásárolt mennyiség
x=7800:0,94\approx 8298 \text{ }cm^3,ami 8,3 liter. Tehát 8,3 litert kell vásárolni.
A feladat c) része
c) A felhasznált papírmennyiség kiszámításához meg kell határoznunk a gúla felszínét. Ehhez viszont szükségünk van a gúla oldallapjának alapélhez tartozó magassságára.
Ennek kiszámításához készítsünk ábrát. Legyen a BC alapél felezőpontja F.
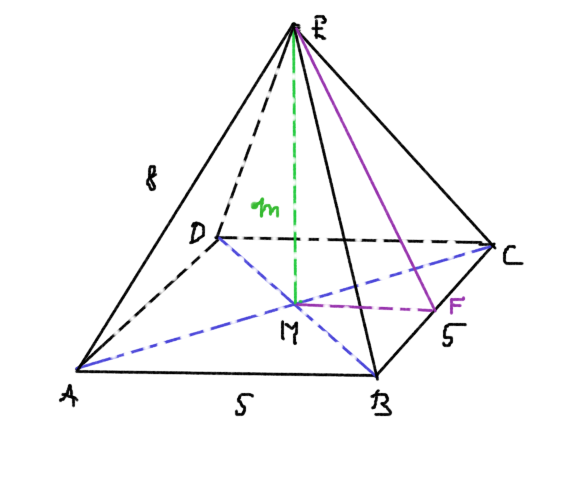
Az EF oldallap magasságot az EMF derékszögű háromszögből számolhatjuk ki Pitagorasz-tétel felhasználásával:
m_o^2=EF^2=m^2+MF^2=51,5+2,5^2=57,75,
ahonnan az oldallap alapélhez tartozó magassága
m_o\approx7,6 \text{ cm }.Tehát a gúla oldallapjának az alapélhez tartozó magassága 7,6 cm. Ezek után a gúla felszíne
A=a^2+4\cdot \frac{a\cdot m_o}{2}=25+2\cdot5\cdot7,6=101 \text{ }cm^2.
A csomagoló papír területe ennek a 136%-a, ami 40 db-ra számolva
40\cdot1,36\cdot101\approx 5494 \text{ } cm^2.Tehát a csomagolópapír területe 5494 cm2. Ezzel a feladatot megoldottuk.
***
Pitagorasz-tétel az emelt szintű feladatokban
Síkgeometriai feladatok
Négyzet
- 7. feladat: (2013. május emelt szintű érettségi 6. feladat a) része) Egy 1 méter oldalú négyzetbe egy második négyzetet rajzoltunk úgy, hogy a belsőnégyzet minden csúcsa illeszkedjen a külső négyzet egy-egy oldalára. A belső és a külső négyzet oldalainak aránya 5 : 7. Milyen arányban osztja két részre a belső négyzet csúcsa a külső négyzet oldalát? Az arány pontos értékét adja meg!
Megoldás: Készítsünk ábrát! Legyenek a nagy négyzet csúcsai ABCD és a beleírt négyzeté JLMN. MIvel a nagy négyzet oldala 1 méter és a kis négyzeté ennek 5/7-ed része, ezért a JLMN négyzet oldala 5/7 méter. Legyen az ABCD négyzet oldalain létrejövő szakaszok hossza x, illetve 1-x. Ez minden oldalon ugyanekkora, hisz a JLMN négyzet az ABCD négyzetből olyan derékszögű háromszögeket vág le, melyek hegyesszögei páronként egyenlőek és átfogójuk is egyenlő, tehát egybevágók.
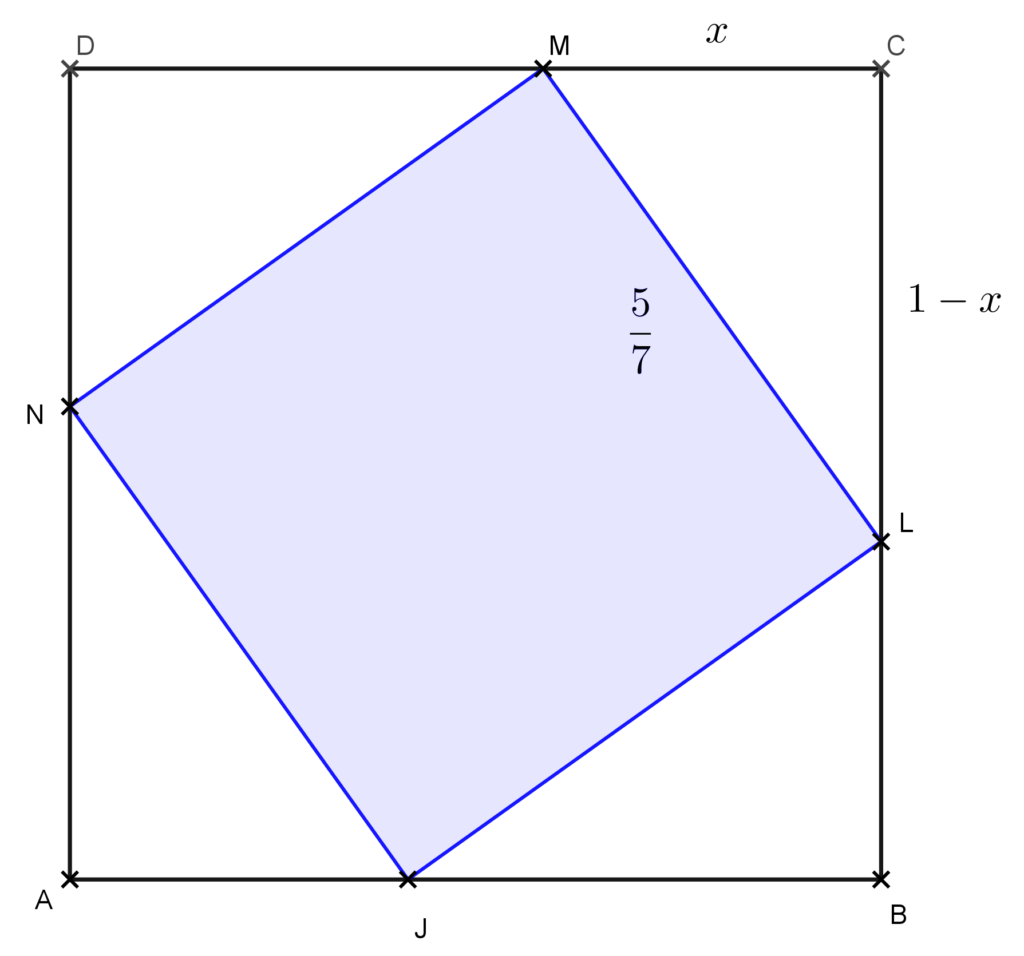
Pitagorasz-tétel alapján:
x^2+(1-x)^2=\frac{25}{49}.Végezzük el a zárójelek felbontását és redukáljunk nullára:
x^2+1-2x+x^2=\frac{25}{49},2x^2-2x+\frac{24}{49}=0.A megoldásokat kiszámolhatjuk a másodfokú egyenlet megoldóképletével. Ezzel kapcsolatosan ajánljuk a másodfokú egyenletekkel foglelkozó cikkünket, melyet a Másodfokú egyenletek linken lehet elérni.
A megoldások
x_1=\frac{4}{7} \text{ } \text{ és } \text{ } x_2=\frac {3}{7}.Így
1-x_1=\frac{3}{7} \text{ } \text{ és } \text{ } 1-x_2=\frac {4}{7}.Mivel az ábra szerint x<1-x, így legyen
x=\frac{3}{7} \text{ } \text{ és } \text{ } 1-x=\frac {4}{7}.Így
\frac{x}{1-x}=\frac{\frac{3}{7}}{\frac{4}{7}}=\frac{3}{4}.Tehát a kérdezet arány 3:4.
***
Téglalap
- 8. feladat: (2015. május matematika emelt szintű érettségi, 2. feladat) Egy televíziókészülék termékleírásában szereplő „16:9-es típus” azt adja meg, hogy mennyi a téglalap alakú tv-képernyő két szomszédos oldalhosszának aránya, a „40 colos” jellemző pedig a képernyő átlójának a hosszát adja meg col-ban (1 col 2,54 cm2 ) .
- a) Számítsa ki a 40 colos, 16:9-es képernyő oldalainak hosszát! Válaszát cm-ben, egy tizedesjegyre kerekítve adja meg!
- b) Két 16:9-es képernyő közül az elsőnek 69%-kal nagyobb a területe, mint a másodiknak. Hány százalékkal nagyobb az első képernyő átlója, mint a másodiké?
Megoldás:
a) Mivel a képernyő oldalainak az aránya 16:9, így az oldalak hossza 16x, illetve 9x. A feltétel szerint a képernyő átlója 40 col, ami centiméterben
40\cdot 2,54=101,6 \text{ cm }.Pitagorasz-tétel felhasználásával számoljuk ki a téglalap oldalait:
(16x)^2+(9x)^2=101,6^2
337x^2=10322,56
x^2=30,63
x=5,535.
Így a képernyő oldalai 16x=88,6 cm és 9x=49,8 cm.
b) Mivel mindkét téglalap oldalainak az aránya 16:9 és szögei páronként egyenlőek, ezért a téglalapok hasonlóak. A feltétel szerint az első téglalap területe 69%-kal nagyobb a második téglalap területénél, ezért a területeik aránya 1,69. Azt tudjuk, hogy hasonló síkidomok területének aránya a hasonlósági arány négyzetével egyenlő, ezért a hasonlósági arány, ami egyben a megfelelő oldalak és átlók arányával is egyenlő
\lambda=\sqrt{1,69}=1,3.Így az első téglalap átlója 30 %-kal nagyobb, mint a második téglalap átlója. Ezzel a feladatot megoldottuk.
***
Térgeometriai feladat
- 9. feladat: (2008. május matematika emelt szintű érettségi, 8. feladat) Az ABCDE szabályos négyoldalú gúla alaplapja az ABCD négyzet, és a gúla alapéle 28 egység hosszú. Legyen F a CE oldalélnek, G pedig a DE oldalélnek a felezőpontja. Ha az ABFG négyszög területe 504 területegység, akkor milyen hosszú a gúla oldaléle?
Megoldás: A részletes megoldást az alábbi videón lehet megtekinteni.
***
Pitagorasz-tétel alkalmazásával kapcsolatosan további feladatok találhatók az alábbi cikkeinkben is:
***
Összefoglalás
A fenti cikkben megfogalmaztuk Pitagorasz tételét és a tétel megfordítását. Az érdeklődők videón megnézhetik mindkét tétel bizonyítását. A cikk második részében 9 feladat nyújt lehetőséget a Pitagorasz-tétel alkalmazására.
Szeretnél még több, hasonló cikket olvasni? Akkor böngéssz a blogunkon Matekos blog!
Ha emelt szintű érettségire készülsz, vagy elsőéves egyetemista vagy? Ekkor ajánljuk figyelmedbe az online tanuló felületünket és a felkészülést segítő csomagjainkat. Az ezekkel kapcsolatos részletekről itt ÉrettségiPro+ olvashatsz.
Összegyűjtöttük az eddigi összes emelt szintű matematika érettségi feladatsort és a megoldásokat. Ezt a gyűjteményt, valamint az érettségire készüléssel kapcsolatos hasznos tanácsokat a Emelt szintű matematika feladatsorok linken érheted el.
Szerző: Ábrahám Gábor (szakmai önéletrajz)
Cikkek
A szerző további cikkei megtalálhatók a Budapesti Fazekas Milyály Gyakorló Általános Iskola és Gimnázium matematika oktatási portálján:
- Feladatok megoldása az analízis eszközeivel.
- Függvény és inverze egyenletekben
- A háromszög területe
- Polinomalgebrai feladatok
- Szélsőértékfeladatok megoldása elemi úton
Az emelt szintű érettségire készüléssel kapcsolatos írásaink a 34 hét alatt új tudás születik, illetve 17 fejezet matematikából linken érhetők el.
A szerző által írt tankönyvek a Maxim Kiadó linken találhatók.
Matek versenyre készülőknek
Ha olyan ambícióid vannak, hogy szeretnél matematikával versenyzés szintjén foglalkozni, akkor javaslom az Erdős Pál Matematikai Tehetségondozó Iskolát. Ezzel vonatkozó részletek ezen linken Erdős Pál Matematikai Tehetséggondozó Iskola olvashatók. A matematika versenyek témáit feldolgozó könyvek, kiadványok (a szerző Egyenlőtlenségek I.-II. című könyvei is) a MATE alapítvány, kiadványok linken kersztül vásárolhatók meg.