A prímszámok a matematika egyik legegyszerűbben megadható, ugyanakkor legizgalmasabb halmazát alkotják. Már több, mint 2000 éve tudjuk, hogy végtelen sok prímszám van, hisz Eukleidész ezt Kr. e. 300-ban bizonyította az Elemek című művében. Ugyanakkor számos megoldatlan probléma létezik ebben a témakörben. Az alábbi cikkben a prímszám definíciója után bemutatunk néhányat közülük. Foglalkozunk a Mersenne- és a Fermat-prímekkel, valamint ismertetünk velük kapcsolatban egy-két fontos tételt. Szó lesz a titkosírásról és a nagy prímszámok kereséséről is. A cikk végén ismertetjük 10 feladat megoldását legegyszerűbbtől az emelt szintig.
Kinek hasznos az alábbi cikkünk?
Neked, ha általános iskolás vagy, és most ismerkedsz a prímszámokkal.
Neked, ha érettségire készülsz, és el szeretnéd mélyíteni a prímszámokkal kapcsolatos ismereteket.
Neked, ha már régebben voltál iskolás, ugyanakkor érdekelnek a prímszámokkal kapcsolatos ismeretek.
A prímszám fogalma
A természetes számokat (nulla és a pozitív egész számok) a pozitív osztóik száma szempontjából négy csoportba soroljuk.
- A 0-nak az összes természetes szám osztója, így végtelen sok pozitív osztója van.
- Az 1-nek egy pozitív osztója van, ez az 1.
- Az olyan pozitív egész számokat, melyeknek pontosan két pozitív osztója van, prímszámoknak nevezzük. Ez a két pozitív osztó az 1 és önmaguk.
- Az olyan pozitív egész számokat, melyeknek kettőnél több pozitív osztója van, összetett számoknak nevezzük.
Tehát a prímszám olyan pozitív egész szám, melynek pontosan két pozitív osztója van. Az 1 nem prímszám, mert pontosan egy pozitív osztója van.
A prímszámokkal kapcsolatosan meg szoktunk adni egy, az előzővel egyenértékű (ekvivalens) definíciót is.
Mielőtt erre rátérnénk, emlékeztetünk arra, hogy ha egy pozitív egész szám osztója egy szorzat valamelyik tényezőjének, akkor osztója a szorzatnak is. Nézzünk erre egy példát: a 14 osztója a 28-nak, így osztója a 28 háromszorosának, azaz a 84-nek is.
Ennek a megfordítása már nem feltétlenül igaz. Azaz, ha egy pozitív egész szám osztója egy szorzatnak, akkor nem biztos, hogy osztója valamelyik tényezőjének. Például 12 osztója a 36–nak, de nem osztója sem a 4-nek, sem a 9-nek. Bizonyítható, hogy a megfordítás az 1-nél nagyobb pozitív egészek közül csak a prímszámokra igaz, ezért fogalmazhatjuk meg az alábbi definíciót.
Eszerint egy 1-nél nagyobb pozitív egész szám akkor és csak akkor prímszám, ha csak úgy lehet osztója két pozitív egész szám szorzatának, ha osztója legalább az egyik tényezőnek.
***
Klasszikus tételek, illetve megoldatlan problémák a prímszámok köréből
A prímszámok száma
Azt már említettük, hogy a prímszámokkal már az ókori görögök is foglalkoztak. Eukleidész Elemek című művében szerepel az alábbi tétel, melynek bizonyítását is ismertetjük.
Tétel: Végtelen sok prímszám létezik.
Bizonyítás: Tegyük fel, hogy nem igaz az állítás, azaz csak véges sok prímszám létezik.
Legyenek ezek
{{p}_{1}},{{p}_{2}},...,{{p}_{n}}.
Képezzük ezekből az alábbi számot
N={{p}_{1}}\cdot {{p}_{2}}\cdot ...\cdot {{p}_{n}}+1.A képzési szabály alapján nyilvánvaló, hogy N a felsorolt n db prímszám egyikével sem osztható. Ugyanakkor N>1, így létezik prímosztója, ami az előzőek szerint különbözik a az eddig felsorolt prímek mindegyikétől, ami ellentmondás. Így a feltevésünk helytelen, tehát végtelen sok prímszám van.
***
Eratoszthenészi szita
Eratoszthenész görög matematikus volt, aki Kr.e. 3. században, Alexandriában élt és tevékenykedett. Foglalkozott csillagászattal és fizikával is. Matematikusként leginkább az ókor három nevezetes problémája érdekelte, azaz a kockakettőzés, a kör négyszögesítése és a szögharmadolás. Az utókor a nevével leginkább a prímszámok kiválogatására használt eljárása kapcsán találkozott, mely Eratoszthenészi szita néven vált ismertté.
Az eljárás lényege a következő. Írjuk fel az egész számokat 1-től N-ig (N>2). Első lépésben áthúzzuk az 1-et és karikázzuk be a 2-t, majd húzzuk át N-ig a 2-nél nagyobb páros számokat. Ezután karikázzuk be a 3-at, majd húzzuk át a három azon többszöröseit N-ig, melyeket még nem húztunk át és nagyobbak 3-nál. Folytassuk tovább az eljárást. Tehát karikázzuk be azt a legkisebb számot, amit eddig nem jelöltünk meg, majd húzzuk át a nála nagyobb többszöröseit.
Ismételjük meg a fenti eljárást mindig a legkisebb még meg nem jelölt számmal. Ha a legkisebb jelöletlen szám nagyobb vagy egyenlő az N négyzetgyökénél, akkor megállunk. Ekkor a bekarikázott és a jelöletlen számok együttesen az N-nél nem nagyobb prímszámok. Itt kihasználtuk azt a tételt, mely szerint, ha N összetett szám, akkor a legkisebb prímosztója nem nagyobb a szám négyzetgyökénél.
Nézzünk erre egy példát. Legyen N=49. Kövessük végig a folyamatot az alábbi ábrasoron.
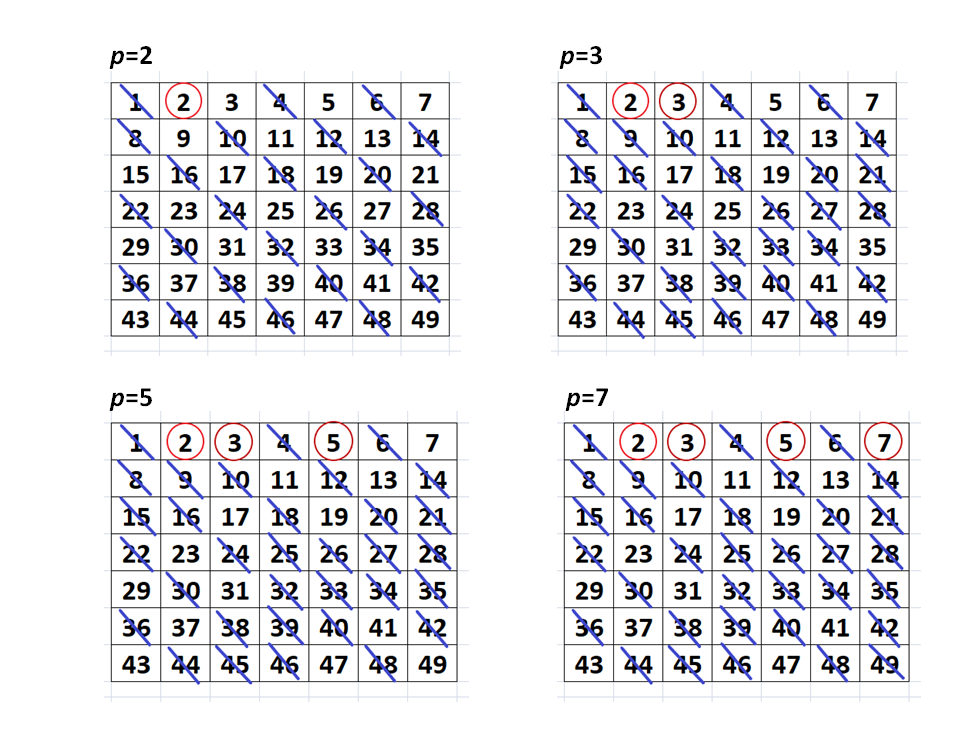
A könnyebb áttekinthetőség kedvéért bekereteztük azokat a ki nem húzott számokat is, amiket korábban nem karikáztunk be. Így a prímszámok N=49-ig az alábbi táblázatban láthatók.
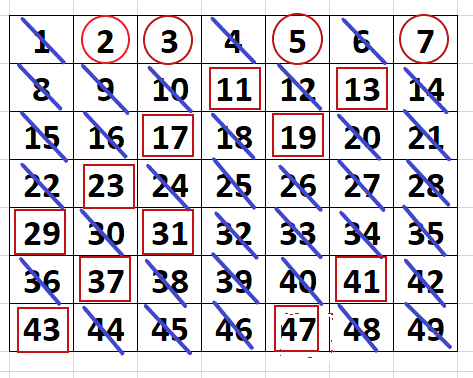
***
Szomszédos prímszámok: ikerprímek
Az előző táblázatban is fellelhetünk olyan prímszámokat, melyek szomszédos páratlan számok. Az ilyen prímeket ikerprímeknek nevezzük. Ezek itt a {3, 5}, {5, 7}, {11, 13}, {17, 19}, {29, 31}, {41, 43}.
Megoldatlan probléma, hogy létezik-e végtelen sok ikerprím pár. Ugyanakkor azt már bizonyították, hogy az ikerprímek „nagyon ritkán” helyezkednek el. Erre utal például az, hogy az ikerprímek reciprokösszege konvergens, míg a prímeké divergens.
Azt is igazolták már, hogy végtelen sok olyan p, p+2 számpár van, ahol p prímszám, míg p+2 prím, vagy két prím szorzata.
A ma (2021. 06. 01.) ismert legnagyobb ikerprímek:
65516468355\cdot {{2}^{333333}}\pm 1.Számjegyeinek a száma 100355. Az aktuálisan ismert legnagyobb ikerprímeket ITT találhatjuk meg.
***
Goldbach-sejtés
Christian Goldbach (1690-1764) német matematikus, a szentpétervári Birodalmi Akadémia tagja volt. Königsbergben született, majd 1725-től haláláig Oroszországban élt.
1724-ben egy Eulerhez írt levelében fogalmazta meg, hogy minden 3-nál nagyobb egész szám felírható legfeljebb három prímszám összegeként.
Euler válaszában a következő szerepelt. Az állítás igazolásához elég lenne bebizonyítani, hogy bármely 2-nél nagyobb páros szám felírható két prímszám összegeként: pl. 4=2+2, 6=3+3, 8=5+3, 10=7+3, 12=5+7 stb.
Ezt a problémát szokás Goldbach-sejtésnek nevezni. Említik még páros, illetve erős Goldbach-sejtésként is. Goldbach levelében szereplő állítást pedig páratlan, vagy gyenge Goldbach-sejtésnek.
Ezzel a közel 300 éves problémával kapcsolatosan ma is csak részeredményekkel rendelkezünk. Eddig
4\cdot {{10}^{18}}\text{-nál}kisebb páros számokra igazolták számítógéppel.
***
Prímszámok számtani sorozatokban
Kérdés, hogy létezik-e akármilyen hosszú (nem konstans) számtani sorozat csupa prímszámból?
Nézzünk néhány példát! Háromtagú számtani sorozat: {3, 5, 7}, öttagú: {5, 11, 17, 23, 29}, hattagú: {7, 37, 67, 97, 127, 157}.
2004-ben Ben Greennek és Terence Taonak sikerült bebizonyítani, hogy a kérdésre adott válasz: igen. A bizonyítás 49 oldalas és magasabb matematikai eszközöket alkalmaz, így annak ismertetésétől most eltekintünk.
A ma ismert leghosszabb, csupa prímszámból álló számtani sorozatnak 23 tagja van:
56211383760397+44546738095860\cdot k \text{, }k\in \mathbb{N} \text{, } k\le 22.Egy végtelen, nem konstans számtani sorozatnak, viszont már nem lehet minden tagja prímszám. Ennek bizonyítása viszonylag egyszerű, ezért most megismerkedünk vele.
Tétel: Nem létezik olyan végtelen hosszú, d>0 differenciájú számtani sorozat, melynek minden tagja prímszám
Bizonyítás:
Legyen a számtani sorozat első tagja a1=p, ahol p prímszám és a differenciája d>0 egész szám. Tekintsük a számtani sorozat p+1-edik tagját, ami
a_{p+1}=p+p \cdot d=p(1+d). Ez a szám viszont összetett, hisz felírható két 1-nél nagyobb pozitív egész szám szorzataként. Ezzel az állítást bizonyítottuk.
Ugyanakkor ismert az alábbi, Dirichlettől származó tétel, ami arról szól, hogy vannak olyan számtani sorozatok, melyeknek végtelen sok tagja prímszám.
Dirichlet-tétel: Ha d>0 és a egész számok relatív prímek, akkor az
{a}_{n}=a+(n-1)dszámtani sorozat végtelen sok prímszámot tartalmaz.
Megmelítjük ennek a tételnek két speciális esetét. Az egyik, hogy végtelen sok 4k+3 alakú prímszám van. A másik szerint 4k+1 (k pozitív egész szám) alakú prímszámból is végtelen sok van. Ezeket az állításokat már nem nehéz bizonyítani, főleg az elsőt.
***
Létezik-e képlet prímszámok előállítására?
Vagyis megadható-e olyan, a természetes ,vagy a pozitív egész számok halmazán értelmezett függvény, amelynek minden helyettesítési értéke prímszám?
Úgy tűnik, hogy ilyenre nem igazán van remény.
Érdekességképpen megemlítjük, hogy Eulertől származik a
p(n)={{n}^{2}}+n+41összefüggés, aminek az n=0, 1, 2, 3, …, 39 esetén vett helyettesítési értéke prím. Ugyanakkor könnyen igazolható, hogy n=40-nél már nem prím.
Speciális alakú prímszámok, tökéletes számok
Ebben a részben a
{2}^{n}+1 \text{, illetve a }{2}^{n}-1 alakú prímszámokkal foglalkozunk. Az előbbieket Fermat-, az utóbbiakat Mersenne-féle prímeknek nevezzük.
Fermat-féle prímszámok
Be lehet bizonyítani (lásd a 9. feladatot), hogy ha egy
{2}^{n}+1alakú szám prím, akkor szükségképpen
n={{2}^{k}}.Az
{{F}_{k}}={{2}^{{{2}^{k}}}}+1alakú számokat Fermat-féle számoknak nevezzük.
Pierre Fermat (1601-1665) Toulouse város közigazgatási szervezetének jogi tanácsosa volt, csak szabadidejében foglalkozott matematikával és fizikával. Így is korának legkitűnőbb matematikusai közé tartozott. Számos tétel fűződik a nevéhez a számelmélet témaköréből, ugyanakkor rendkívül értékes megfigyeléseket végzett a geometriában és az infinitezimális számítás előkészítésében.
Fermat úgy vélte, hogy Fk a k minden nemnegatív egész értéke esetén prímszámot ad. Ez igaz is k=0, 1, 2, 3, 4 esetén, ugyanakkor
F_5=2^{2^5}+1=2^{32}+1nem prím, hisz osztható 641-gyel, mint ahogy ezt már Euler 1732-ben, 25 éves korában bebizonyította.
A Fermat-prímek alkalmazása
Azt már bizonyították, hogy az 5 és 32 közé eső pozitív egész k-k esetén Fk összetett szám. Egyelőre nem találtak k>4 esetén a Fermat-számok között prímet. Egy-egy ilyen gondolatkör kapcsán a laikusokban mindig felmerül a kérdés, hogy van-e értelme ezzel foglalkozni? Érdemes-e további Fermat-prímeket keresni?
A Fermat-prímek jelentőségére Gauss világított rá a szabályos sokszögek szerkeszthetőségére vonatkozó alábbi tételével.
Tétel: Egy szabályos n-szög akkor és csak akkor szerkeszthető körzővel és egyélű vonalzóval, ha
n={{2}^{k}}\cdot {{p}_{1}}\cdot {{p}_{2}}\cdot ...\cdot {{p}_{r}}ahol k természetes szám, és p1, p2,…, pr páronként különböző Fermat-féle prímek.
Eszerint szerkeszthető pl. szabályos háromszög, ötszög, hatszög, tízszög, tizenkétszög, tizenötszög, tizenhétszög stb.
Mesrenne-féle prímszámok
Bizonyítható, hogy ha egy
{2}^{n}-1alakú szám prímszám, akkor n is prím (lásd a 10. feladatot).
Az
M_p={2}^{p}-1alakú számokat, ahol p prímszám, Mersenne-féle számoknak, közülük a prímeket Mersenne-prímeknek nevezzük. A legkisebb olyan Mersenne-szám, ami nem prímszám az M11=2047, ami felírható 23 és 89 szorzataként. Jelenleg, azaz 2021. 06. 01. napján 51 darab Mersenne-prímet ismerünk. Az aktuálisan ismert legnagyobb prímet ITT találhatjuk meg.
Marin Mersenne (1588-1648) francia matematikus, minorita szerzetes. Nagy érdeme volt abban, hogy korának matematikusai értesültek egymás eredményeiről, mert szinte minden jelentős matematikussal levelezésben állt.
A Mersenne-prímek jelentőségét a prímszámkeresésben betöltött szerepük, valamint a páros tökéletes számokkal való kapcsolatuk adja. A ma ismert legnagyobb prímszám is Mersenne-prím.
Tökéletes számok
Egy pozitív egész számot tökéletes számnak nevezünk, ha pozitív osztóinak az összege egyenlő a szám kétszeresével. Pl. a 6 és a 28 is tökéletes szám, hisz 1+2+3+6=12, illetve 1+2+4+7+14+28=56. Már Eukleidész Elemek című művében szerepel egy konstrukció a tökéletes számok előállítására. Az erre vonatkozó állítást Euler tovább fejlesztette és így alakult ki az alábbi Eukleidész-Euler-tétel.
Tétel: Egy n páros szám akkor és csak akkor tökéletes szám, ha
n={{2}^{p-1}}\left( {{2}^{p}}-1 \right),ahol Mp=2p-1 Mersenne-féle prím, így p prímszám.
A tételből következik, hogy pontosan annyi páros tökéletes szám van, mint ahány Mersenne-prím. Mivel nem tudjuk, hogy az utóbbiból végtelen sok van-e, így az is megoldatlan probléma, hogy végtelen sok tökéletes szám van-e. Az is nyitott kérdés, hogy van-e egyáltalán páratlan tökéletes szám.
***
Prímtesztek, néhány szó a titkosírásról
Mennyire nehéz eldönteni egy pozitív egész számról, hogy prímszám-e? Mennyi ideig tart egy összetett szám prímtényezős felbontása?
Ezekre a kérdésekre látszólag egyszerűnek tűnik a válasz.
Például prímszám-e az 523?
A korábbiak alapján elég megnézni, hogy az 523 négyzetgyökéig létezik-e olyan prímszám, amely osztója az 523-nak. Mivel ez a szám 22 és 23 közé esik, ezért elég megnézni, hogy a 2, 3, 5, 7, 11, 13, 17, 19 számok valamelyike osztója-e az 523-nak. Az oszthatósági szabályok alapján a 2, 3, 5 és 11 gyorsan kizárható. A maradék mindegyikével elosztva, kiderül, hogy a hányados egyik esetben sem egész szám, így az 523 prímszám.
Ez nem tartott sokáig. Ugyanakkor mit mondhatunk akkor, ha a vizsgált szám több ezer, vagy több tízezer jegyű? Akkor is hatékony ez az eljárás?
Ilyen nagy számok esetén a fenti eljárás a jelenlegi technikai eszközökkel kivitelezhetetlen, mert nagyon sok időt venne igénybe. Például egy 1000 jegyű számot, amelynek nincs kis prímosztója, vagy valamilyen speciális tulajdonsága, évmilliárdok alatt sem lehet tényezőkre bontani.
Milyen hatékony eljárások léteznek?
Ezeket nevezzük prímteszteknek. Közülük most megemlítünk kettőt, melyek viszonylag könnyen érthetők. Az egyik a Fermat-, a másik a Mersenne-prímek tesztelésére alkalmas
Az első a Pepin-teszt, amely kimondja, hogy egy Fk (0<k) Fermat-féle szám, akkor és csak akkor prím, ha teljesül rá, hogy Fk osztója a
{{3}^{\frac{{{F}_{k}}-1}{2}}}+1számnak.
A második a Lucas-Lehmer-teszt. Eszerint ha p>2 prímszám, továbbá
{{a}_{1}}=4 \text{ } \text{ és } \text{ }{{a}_{n+1}}=a_{n}^{2}-2 \text{ } (n\ge 1).Ilyenkor az Mp Mersenne-féle szám, akkor és csak akkor prímszám, ha Mp osztója az ap-1-nek.
A nagy összetett számok nehézkes faktorizációja teszi lehetővé azt, hogy a nagy prímszámokat hatékonyan tudjuk használni titkosírásban, információk titkosításában.
***
Összefoglalás
Igyekeztünk a cikkben néhány érdekességet, fontos információt felvillantani a prímszámokkal kapcsolatosan. A téma nagyon szerteágazó és olykor-olykor mélyre hatoló, ezért nem volt lehetőségünk mindenre kitérni. Akit további részletek is érdekelnek, annak javaslom Freud Róbert és Gyarmati Edit Számelmélet című könyvét.
Prímszámokkal kapcsolatos feladatok és azok megoldásai a Matekos blogban cikkünkben ITT érhetők el.
Szeretnél még több, hasonló cikket olvasni? Akkor böngéssz a blogunkon Matekos blog!
Emelt szintű érettségire készülsz, vagy elsőéves egyetemista vagy? Ekkor ajánljuk figyelmedbe az online tanuló felületünket és a felkészülést segítő csomagjainkat. Az ezekkel kapcsolatos részletekről itt ÉrettségiPro+ olvashatsz.
Összegyűjtöttük az eddigi összes emelt szintű matematika érettségi feladatsort és a megoldásokat. Ezt a gyűjteményt, valamint az érettségire készüléssel kapcsolatos hasznos tanácsokat a Emelt szintű matematika feladatsorok linken érheted el.
Szerző: Ábrahám Gábor (szakmai önéletrajz)

