Mivel a rombusz speciális paralalogramma és deltoid is, ezért a tisztelt Olvasó figyelmébe ajánljuk a velük kapcsolatos cikkeinket. A paralelogrammákról szóló cikk a Paralelogramma, míg a deltoidokról szóló a Deltoid linken érhető el.
Ebben a cikkben foglalkozunk a rombusz definíciójával és tulajdonságaival. Képletet adunk a területének és kerületének kiszámítására, majd öt feladaton kersztül alkalmazzuk a tanultakat.
Kinek ajánljuk a cikkünket?
Neked, ha általános iskolás vagy, és most ismerkedsz a négyszögfajtákkal.
Neked, ha érettségire készülsz, és nagyobb jártasságra szeretnél szert tenni síkgeometriából.
Neked, ha esetleg már régebben voltál iskolás, ugyanakkor valamiért most szükséged lenne rombuszokkal kapcsolatos ismeretekre, és szeretnéd feleleveníteni azokat.
Mi segítünk! Olvasd el cikkünket, és megtalálod a választ kérdéseidre.
***
A rombusz fogalma és tulajdonságai
A rombusz fogalma
A rombusz olyan négyszög, melynek oldalai egyenlők.
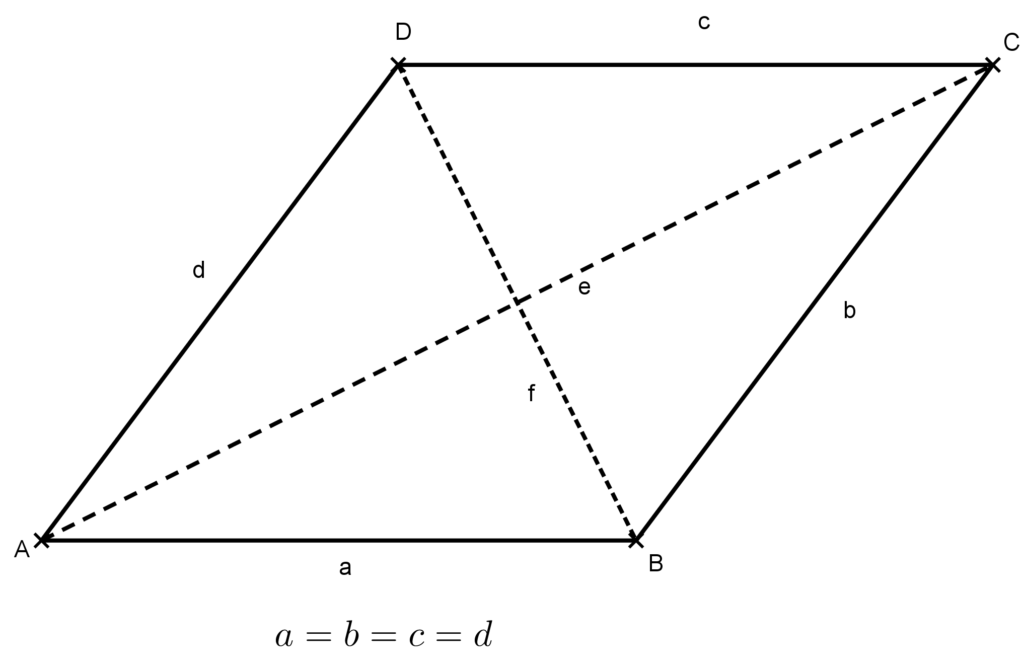
Az olyan rombuszt, melynek szögei egyenlők, négyzetnek nevezzük. Így a négyzet olyan négyszög, melynek oldalai egyenlő hosszúak és szögei egyenlő nagyságúak.
***
A rombusz tulajdonságai
Mivel a rombuszok a paralelogrammák és deltoidok halmazának is elemei, ezért a két négyszögre jellemző tulajdonságok mindegyikével rendelkezik.
Eszerint tehát a rombusz
- szemközti oldalai párhuzamosak;
- szemközti szögei egyenlő nagyságúak;
- bármely két szomszédos szögének összege 180°;
- átlói merőlegesen felezik egymást;
- középpontosan szimmetrikus;
- mindkét átlójára nézve tengelyesen szimmetrikus;
- egyben érintőnégyszög is.
***
Kerülete és területe
A kerülete
Mivel korábban már foglalkoztunk a paralelogramma kerületével, így a speciális négyszögünk kerületét is könnyen megadhatjuk. Mivel az ABCD rombusz oldalainak a hossza AB=BC=BD=DA=a , így a kerülete
K= AB+BC+BD+DA=4a.
***
A területe
Mivel a rombuszok mind a deltoidok, mind a paralelogrammák halmazába beletartoznak, ezért területüket úgy számolhatjuk ki, ahogy ezt az említett négyszögfajták esetében már tanultuk.
Legyen az ABCD rombusz oldalának a hossza a, a hozzá tartozó magassága m. Legyen az A csúcsnál levő szöge α, az átlóinak a hossza e és f. Lásd az ábrát!
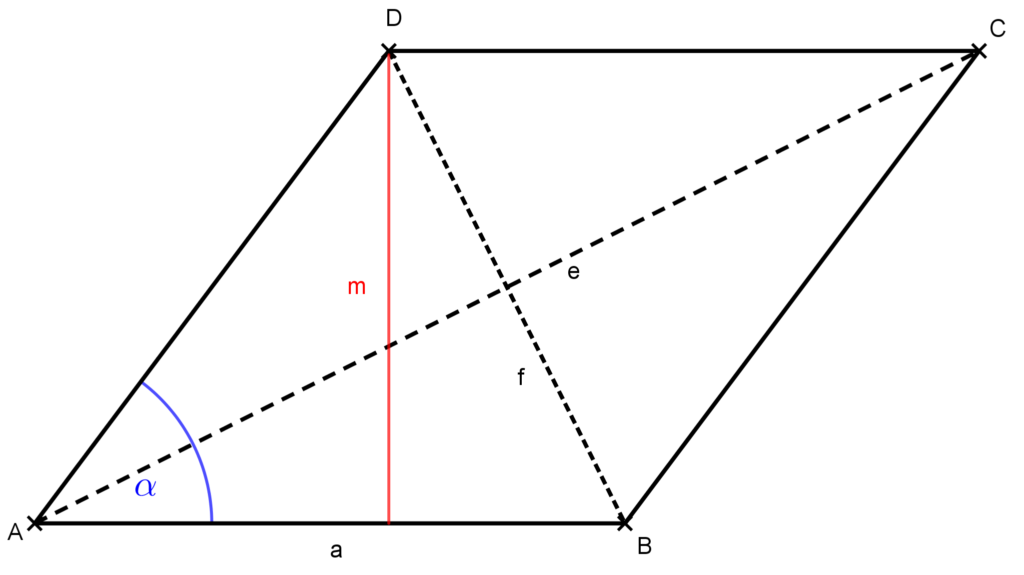
Az eddigiekből következik, hogy a területét az alábbi módokon számolhatjuk ki:
T=a\cdot m=a^2 \cdot \text {sin } \alpha=\frac{e\cdot f}{2}.***
Feladatok rombuszokra
Egyszerű feladatok
- 1. feladat: Az alábbi állítások közül melyik igaz, melyik hamis?
- Minden rombusz trapéz.
- Létezik olyan rombusz, melynek négy szimmetriatengelye van.
- Létezik olyan rombusz melynek magassága ugyanakkora, mint az oldala.
- Minden rombusznak van köré írt köre.
Megoldás:
- Az állítás igaz, mert a trapéz olyan négyszög, melynek van párhuzamos oldalpárja, és a rombusz szemközti oldalai párhuzamosak.
- Az állítás igaz, mert a négyzet ilyen négyszög.
- Az állítás igaz, ugyanis a négyzet rendelkezik ezzel a tulajdonsággal.
- Az állítás hamis, mert csak a négyzet ilyen tulajdonságú rombusz.
***
- 2. feladat: Adott az ABCD rombusz, melynek kerülete 40 cm és két szomszédos szögének aránya 1:2. Mekkorák az oldalai, átlói? Mekkora a területe és a beírt körének sugara?
Megoldás: Legyen az ABCD rombusz oldalának a hossza a. Ekkor K=4a=40, amiből a=10 cm.
Mivel a szomszédos szögek aránya 1:2 és a tudjuk, hogy ezek ősszege 180°, ezért a kisebbik szög α=60°. Készítsünk ábrát.
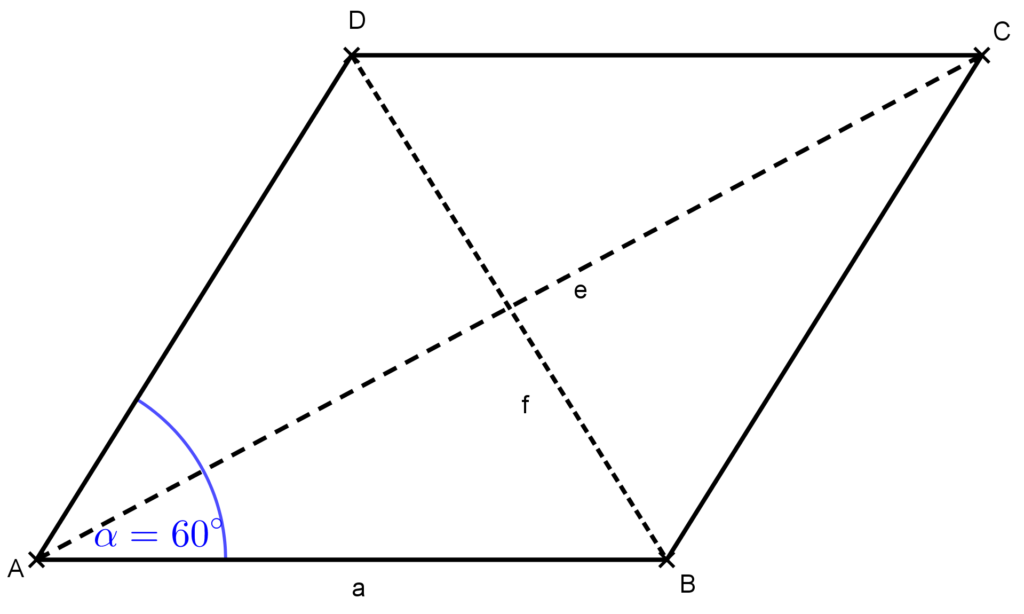
Az ABD háromszög egyenlőszárú és szárszöge 60°-os, ezért szabályos. Ebből következik, hogy kisebb átlójának a hossza f=10 cm.
Mivel az átlói merőlegesen felezik egymást, ezért a hosszabbik átló felét kiszámolhatjuk Pitagorasz-tétellel, vagy felhasználhatjuk azt az ismert tényt is, hogy a szabályos háromszög magassága, az oldalának a
\frac{\sqrt{3}}{2}\text{ -szerese}.Ez alapján
e=2\cdot a\cdot \frac{\sqrt{3}}{2}=a\cdot \sqrt{3},azaz e=17,32 cm két tizedes jegyre kerekítve.
Számoljuk ki most a területét az átlóiból
T=\frac{e\cdot f}{2}=\frac{10\cdot 17,32}{2}= 86,6 \text{ cm}^2.Beírt körének középpontja az átlói metszéspontja, az átmérője pedig megegyezik a párhuzamos oldalainak a távolságával, azaz a magasságával. Ez a magasság egyben az ABD szabályos háromszög magassága is, így
r=\frac{m}{2}=\frac{a\cdot \frac{\sqrt{3}}{2}}{2}=a\cdot \frac{\sqrt{3}}{4}=5\cdot \frac{\sqrt{3}}{2} \approx 4,33 \text{ cm}.Ezzel a feladatot megoldottuk.
***
Nehezebb feladatok
- 3. feladat: (középszintű érettségi feladat 2007. október)
Egy négyzet és egy rombusz egyik oldala közös, a közös oldal 13 cm hosszú. A négyzet és a rombusz területének az aránya 2:1.
a) Mekkora a rombusz magassága?
b) Mekkorák a rombusz szögei?
c) Milyen hosszú a rombusz hosszabbik átlója? A választ két tizedes jegyre kerekítve adja meg!
Megoldás:
a) Készítsünk ábrát!
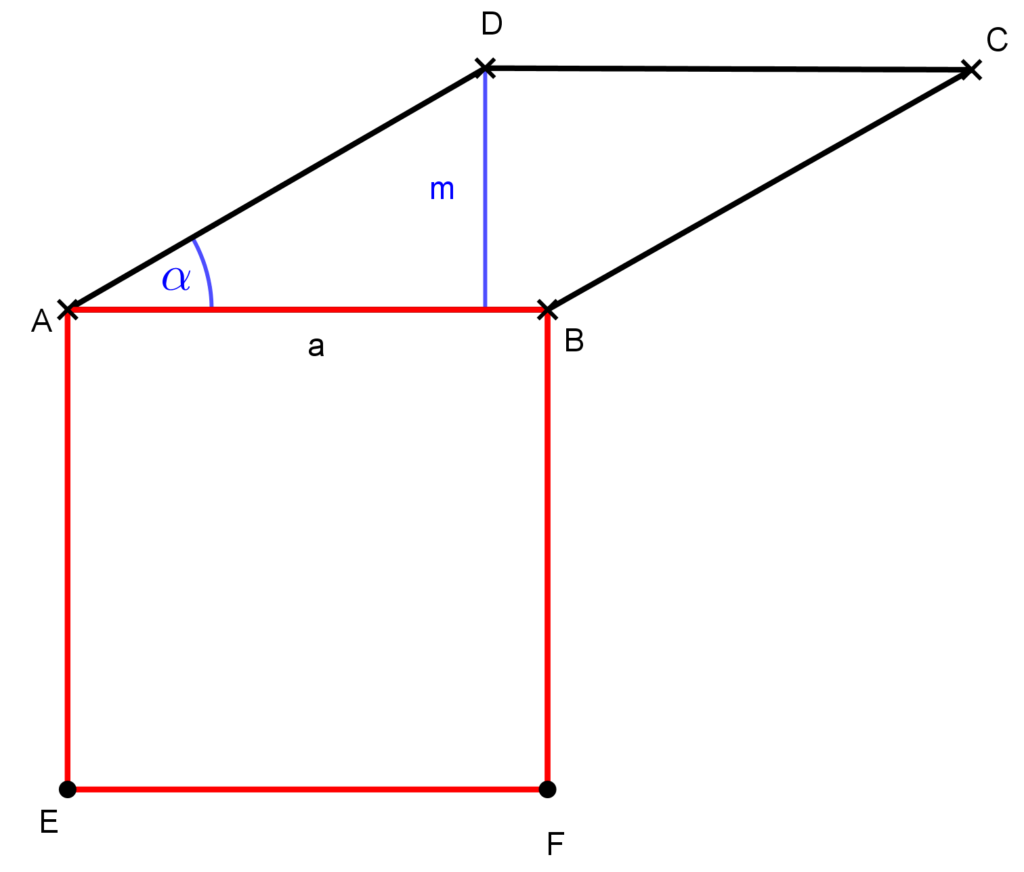
A négyzet, illetve a rombusz oldala az ábrának megfelelően legyen a, a rombusz magassága m. Ezen adatokat felhasználva felírhatjuk a két négyszög területének az arányát
\frac{T_{rombusz}}{T_{négyzet}}=\frac{a\cdot m}{a^2}=\frac{a}{m}=\frac{1}{2}.Így a magassága m=6,5 cm.
b) Mivel a rombusz m magassága merőleges az a oldalra, így szinusz szögfüggvénnyel kiszámolhatjuk az α szöget
\text{sin }\alpha=\frac{m}{a}=0,5,ahonnan α=30°. Így a B csúcsnál levő szöge 150°.
c) Ennek kiszámításához készítsünk ábrát!
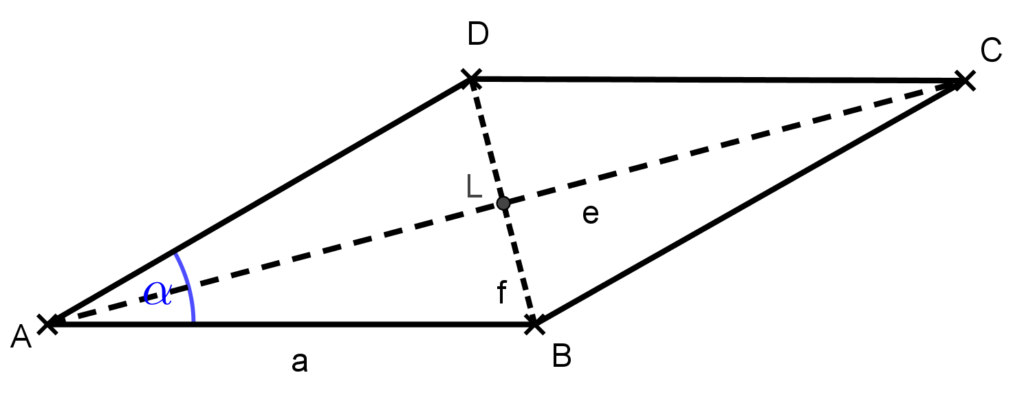
Legyen az átlók metszéspontja L. Számítsuk ki az e átló felét az ABL derékszögű háromszögből koszinusz szögfüggvény felhasználásával, így
\text{cos }\frac{\alpha}{2}=\frac{\frac{e}{2}}{a}=\frac{e}{2a},azaz
e=2a\cdot \text{cos}15°=26\cdot \text{cos}15°\approx 25,11 \text{ cm}Ezzel a feladatot megoldottuk.
***
- 4. feladat: (emelt szintű feladat)
Egy rombusz egyik szöge α, két átlója e és f, kerülete k. Bizonyítsuk be, hogy
\frac{\text{sin }\frac{\alpha}{2}+\text{cos }\frac{\alpha}{2}}{2}=\frac{e+f}{k}.Megoldás: Készítsünk ábrát!
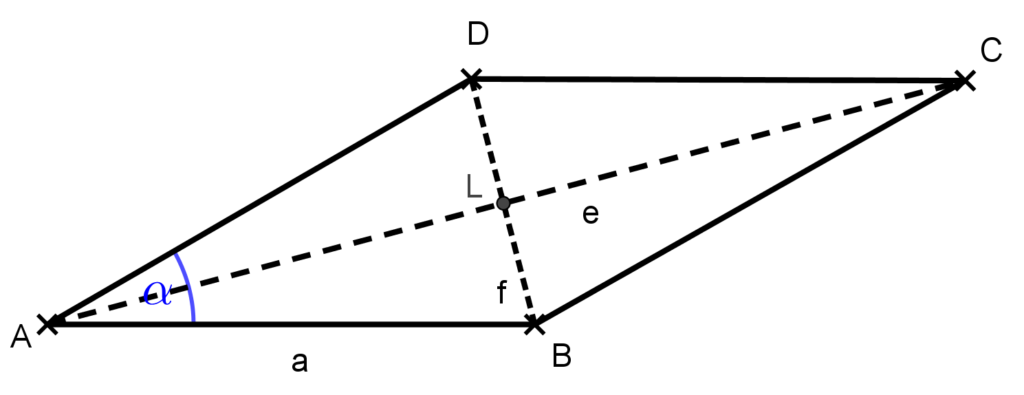
Írjuk fel a szinusz, illetve koszinusz szögfüggvényt az α/2 szögre az ABL derékszögű három szögben.
Így
\text{sin }\frac{\alpha}{2}=\frac{\frac{f}{2}}{a}=\frac{f}{2a},illetve
\text{cos }\frac{\alpha}{2}=\frac{\frac{e}{2}}{a}=\frac{e}{2a}.Ezért
\frac{\text{sin }\frac{\alpha}{2}+\text{cos }\frac{\alpha}{2}}{2}=\frac{\frac{e+f}{2a}}{2}=\frac{e+f}{4a}=\frac{e+f}{k}.Ezt kellett bizonyítani.
***
- 5. feladat: (emelt szintű feladat)
Az ABCD rombusz AC átlójának tetszőleges belső pontja P. Bizonyítsuk be, hogy
AB^2-PB^2=AP\cdot PC.
Megoldás: Készítsünk ábrát! Az általánosságot nem szorítja meg, ha a P pontot az AL szakaszon (eshet az L pontba is) vesszük fel. Mivel az állításban a PB szakasz is szerepel, ezért kössük össze P-t a B csúccsal!
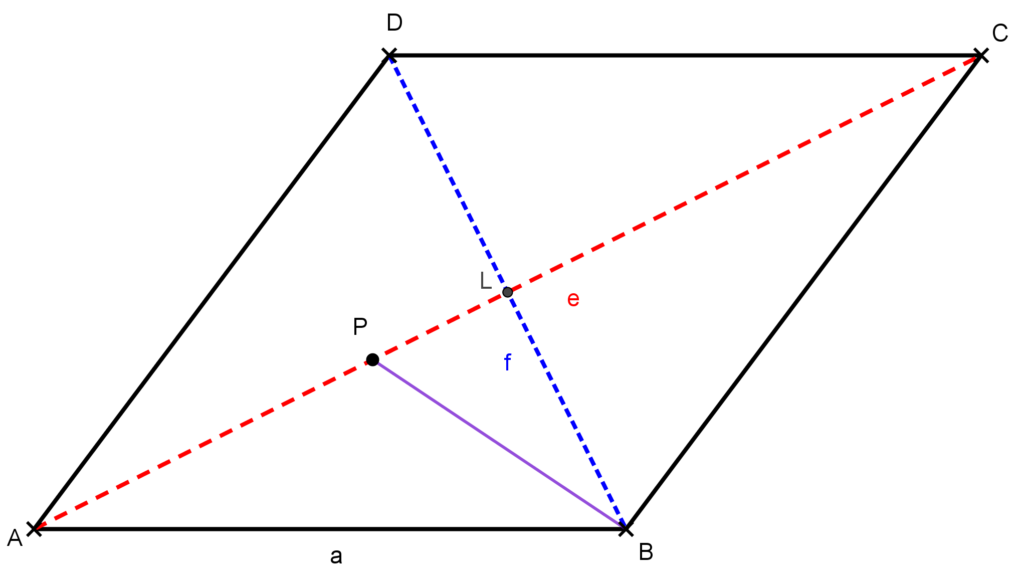
Ha a P és L pontok nem esnek egybe, akkor a PBL háromszög derékszögű, így használjuk Pitagorasz tételét:
PB^2=PL^2+LB^2=\left(PC-\frac{AC}{2} \right)^2+\left(\frac{BD}{2} \right)^2.Ha P=L, akkor PL=0, így PB=LB. Az előző összefüggés, akkor is fennáll.
Végezzük el a zárójelek felbontását, így kapjuk, hogy
PB^2=PC^2-2PC\cdot\frac{AC}{2} +\left(\frac{AC}{2} \right)^2+\left(\frac{BD}{2} \right)^2.Mivel az ABL háromszög is derékszögű, ezért számolhatunk a Pitagorasz-tétellel.
Ez alapján írhatjuk, hogy
\left(\frac{AC}{2} \right)^2+\left(\frac{BD}{2} \right)^2=AB^2.Így
PB^2=PC^2-PC\cdot AC +{AB}^{2} ,azaz
PC(AC-PC)=AB^2-PB^2,
használjuk fel, hogy AP=AC–PC, így
PC\cdot AP=AB^2-PB^2,
Ezt kellett bizonyítani.
***
Összefoglalás
A fenti cikkben megismerkedtünk a rombusz definíciójával, tulajdonságaival, kerületének és területének kiszámítási módjával. Tudjuk, hogy a rombuszok halmaza a paralelogrammák és a deltoidok halmazának metszete. Ezért a rombuszok rendelkeznek mindazon tulajdonságokkal, amikkel a paralelogrammák és deltoidok is. Mint láttuk alkalmaztuk a tanult ismereteket öt, fokozatosan nehezedő feladatban.
Szeretnél még több, hasonló cikket olvasni? Akkor böngéssz a blogunkon Matekos blog!
Emelt szintű érettségire készülsz, vagy elsőéves egyetemista vagy? Ekkor ajánljuk figyelmedbe az online tanuló felületünket és a felkészülést segítő csomagjainkat. Az ezekkel kapcsolatos részletekről itt ÉrettségiPro+ olvashatsz.
Összegyűjtöttük az eddigi összes emelt szintű matematika érettségi feladatsort és a megoldásokat. Ezt a gyűjteményt, valamint az érettségire készüléssel kapcsolatos hasznos tanácsokat a Emelt szintű matematika feladatsorok linken érheted el.
Szerző: Ábrahám Gábor (szakmai önéletrajz)
Cikkek
A szerző további cikkei megtalálhatók a Budapesti Fazekas Milyály Gyakorló Általános Iskola és Gimnázium matematika oktatási portálján:
- Feladatok megoldása az analízis eszközeivel.
- Függvény és inverze egyenletekben
- A háromszög területe
- Polinomalgebrai feladatok
- Szélsőértékfeladatok megoldása elemi úton
Az emelt szintű érettségire készüléssel kapcsolatos írásaink a 34 hét alatt új tudás születik, illetve 17 fejezet matematikából linken érhetők el.
A szerző által írt tankönyvek a Maxim Kiadó linken találhatók.
Matek versenyre készülőknek
Ha olyan ambícióid vannak, hogy szeretnél matematikával versenyzés szintjén foglalkozni, akkor javaslom az Erdős Pál Matematikai Tehetségondozó Iskolát. Ezzel vonatkozó részletek ezen linken Erdős Pál Matematikai Tehetséggondozó Iskola olvashatók. A matematika versenyek témáit feldolgozó könyvek, kiadványok (a szerző Egyenlőtlenségek I.-II. című könyvei is) a MATE alapítvány, kiadványok linken kersztül vásárolhatók meg.

