Sorozatok határértéke – emelt szintű matek

A sorozatok határáértéke lehet véges, illetve végtelen, mínusz végtelen. Ha a sorozat határértéke véges, akkor a sorozat konvergens, ha végtelen, akkor a sorozatot divergensnek hívjuk, de ilyenkor szokás valódi divergens sorozatnak is nevezni. Az alábbi cikkben ezeket a fogalmakat építjük fel szemléletes példákon keresztül. Ezután foglalkozunk a konvergens sorozatok két fontos tulajdonságval, a sorozatok határértéke közötti műveletekkel, és megoldunk néhány példát.

A cikk elsősorban a témakör emelt szintű érettségihez kapcsolódó részét taglalja. Így ha valaki szeretne ennél jobban elmerülni a sorozatok határértéke című fejezetben, annak ajánljuk a youtube csatornánkon a Sorozatok emelt szintű érettségin című lejátszási listát, amit ITT lehet elérni.

Azoknak, akik jártasságot szeretnének szerezni a témakörhöz tartozó feladatok megoldása terén, azoknak ajánjuk az online tanulófelületünket. Erről bővebben ITT, a tananyag felépítéséről pedig ITT lehet olvasni.

Kiknek ajánljuk a Sorozatok határértéke című cikket?

Természetesen azoknak, akik emelt szintű matematika érettségire készülnek. Emellett azoknak is, akik középszinten érettségiztek matematikából, ugyanakkor olyan szakon tanulnak tovább, ahol a matematika, a kalkulus vagy analízis előkerül tantárgyként.

***

Konvergens számsorozatok

Bevezető feladatok

• 1. példa: Legyen adott az

a_n=\frac{n+(-1)^n}{n}

sorozat. Adjuk meg és ábrázoljuk számegyenesen a sorozat első hat tagját!

Megoldás:

A sorozat első hat tagja:

a_1=\frac{1+-1}{1}=0,\text{ }a_2=\frac{2+(-1)^2}{2}=\frac{3}{2}, \text{ }a_3=\frac{3+(-1)^3}{3}=\frac{2}{3}

a_4=\frac{4+(-1)^4}{4}=\frac{5}{4}, \text{ }a_5=\frac{5+(-1)^5}{5}=\frac{4}{5}, \text{ } a_6=\frac{6+(-1)^6}{6}=\frac{7}{6}.

Ábrázoljuk a kiszámolt tagokat számegyenesen!

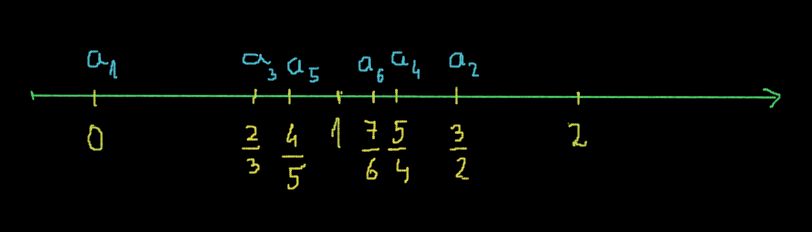
Ezzel a feladatot megoldottuk.

***

A szemléletes megközetés alapján úgy tűnik, hogy a sorozat tagjai egyre közelebb kerülnek az 1-hez. Hogy lehetne ezt a szemléletet matematikailag, precízen megközelíteni? Ebben nyújt segítséget a következő feladat.

• 2. példa: Legyen adott az

a_n=\frac{n+(-1)^n}{n}

sorozat. Mely pozitív egész n-től teljesül, hogy

\text{a)} \text{ } |a_n-1|<\frac{1}{10^{12}}\text{ }\text{ b)}\text{ }|a_n-1|<\epsilon,

ahol ε tetszóleges pozitív valós szám?

Megoldás:

a) Az abszolútérték szemléletes jelentése szerint azt kell meghatároznunk, hogy a sorozat hanyadik tagjától teljesül, hogy a számegyenesen a sorozat tagjainak az 1-től való “távolsága” kisebb, mint a megadott érték.

Eszerint

|a_n-1|=\left|\frac{n+(-1)^n}{n}-1\right|=\left|\frac{n+(-1)^n-n}{n}\right|=\left|\frac{(-1)^n}{n}\right|=\frac{1}{n}<\frac{1}{10^{12}}.

Az utolsó egyenlőtlenséget figyelembe véve ez pontosan akkor teljesül, ha

10^{12}< n,

a 10¹²+1-edik tagtól kezdve.

Ez azt jelenti, hogy ha 10¹²<n, akkor

|a_n-1|<\frac{1}{10^{12}},

azaz

-\frac{1}{10^{12}}< a_n-1<\frac{1}{10^{12}},

vagyis

1-\frac{1}{10^{12}}< a_n<1+\frac{1}{10^{12}}.

Az N=10¹² értéket küszöbszámnak nevezzük.

Ez azzal egyenértékű, hogy ha 10¹² <n, akkor

a_n\in \left]1-\frac{1}{10^{12}};1+\frac{1}{10^{12}}\right[ 

azaz benne van az 1-nek a 10^-12 sugarú környezetében.

Jelenítsük meg ezt a számegyenesen:

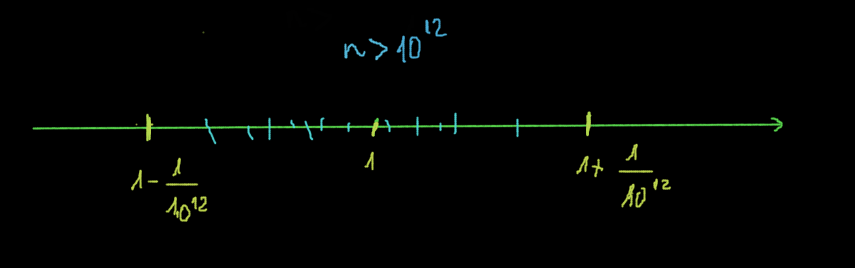
A kék vonások szemléltetik a sorozattagokat.

b)

Ebben a részben csak annyi változás van, hogy a 10^-12 helyett pozitív ε szerepel. Ez a levezetés lényegén nem módosít.

Így

|a_n-1|=\left|\frac{n+(-1)^n}{n}-1\right|=\frac{1}{n}< \epsilon.

Ez pontosan akkor teljesül, ha

\frac{1}{\epsilon}< n.

Az

N=\frac{1}{\epsilon}

értéket küszöbszámnak nevezzük.

Ez tehát azt jelenti, hogy ha

N=\frac{1}{\epsilon}< n,

akkor

|a_n-1|<\epsilon,

azaz

a_n\in \left]1-\epsilon;1+\epsilon\right[

intervallumban, vagyis az 1 ε sugarú környezetében.

Ez a kijelentés egyenértékű azzal is, hogy bármely pozitív ε esetén az 1 ε sugarú környezetén kívül csak véges sok tagja van a sorozatnak.

Ezzel ezt a feladatot megoldottuk.

***

Ha az a_n sorozat olyan tulajdonságú, mint azt a feladat b) részében láttuk, akkor az a_n sorozatra azt mondjuk, hogy konvergens és határértke 1.

Ezt úgy jelöljük, hogy

\lim_{n\rightarrow\infty}a_n=1.

A konvergens sorozat definíciója

Most fogalmazzuk meg a konvergens sorozat két egymással egyenértékű (ekvivalens) definícióját.

• 1.definíció: Az (a_n) sorozat konvergens és határértéke A, ha bármely 0<ε esetén létezik olyan N (ε-tól függő) küszöbszám, hogy ha n>N, akkor

|a_n-A|<\epsilon.

• 2. definíció: Az (a_n) sorozat konvergens és határértéke A, ha bármely 0<ε esetén az (a_n) sorozatnak csak véges sok tagja van az A ε sugarú környezetén kívül.

Jelölés:

\lim_{n\rightarrow\infty}a_n=A.

Ha egy sorozat nem konvergens, akkor divergensnek nevezzük.

***

Konvergens sorozatok két tulajdonsága

A nyitó példában szereplő sorozatról beláttuk, hogy konvergens és a határértke 1.

Milyen fontos tulajdonsággal rendelkezik még az a sorozat. Könnyen láthatjuk, hogy korlátos is. Egy alsó korlátja a 0, egy felső pedig pl. a 2.

Vajon az minden konvergens sorozatra igaz, hogy korlátos? Igen ez bizonyítható. Most csak a tételt mondjuk ki, a bizonytást nem közöljük, csak belinkeljük azt a youtube csatornánk erre vonatkozó videóját.

Első tulajdonság

Tétel: Ha az (a_n) sorozat konvergens, akkor korlátos.

Bizonyítás: A bizonyítást megtalálod ITT.

• 1. Megjegyzés:

A tétel azt mondja ki, hogy a sorozatok konvergenciájából következik a korlátos tulajdonságuk. Ez azt jelenti, hogy a korlátosság a konvergencia szükséges feltétele. Tehát ha egy sorozat nem korlátos, akkor nem lehet konvergens. Vajon elégséges feltétel is? Erre a kérdésre egy példával válaszolhatunk. Tekintsük az

a_n=(-1)^n

sorozatot. Ez a sorozat korlátos, ugyanakkor könnyű róla bebizonyítani, hogy nem konvergens. Ennek bizonyításában segít a következő alfejezetben szereplő tétel is.

• 2. megjegyzés:

Van-e olyan tétel,ami elégséges feltételt biztosít a konvergenciához. Igen ilyen tétel létezik és az alábbi módon fogalmazható meg.

Tétel: Ha egy sorozat monoton és korlátos, akkor konvergens is. Ha monoton növekvő, akkor a legkisebb felső korlátjához, ha monoton csökkenő, akkor a legnagyobb alsó korlátjához konvergál.

Bizonyítás: A tételt most nem bizonyítjuk, ugyanakkor elérhető a youtube csatornánkon ITT.

Második tulajdonság

Vajon a konvergens sorozatok határértéke egyértelműen meghatározott? Az eddigi példák és definició is azt sejtetei, hogy igen.

Tétel: Bármely konvergens sorozatnak egy határértéke van.

Bizonyítás: A bizonyítás ITT érhető el.

***

Műveletek konvergens sorozatok között

Két sorozat között értelmezhetünk műveleteket. Ezek az összeadás (kivonás), a szorzás, valamint bizonyos feltételek között osztást. Ez mindig azt jelenti, hogy a sorozat általános (n-edik) tagjai között elvégezzük a megfelelő műveletet.

A konvergens sorozatok közötti műveletek jól használhatók feladatok megoldására. Erre látunk példákat a Sorozatok határértéke feladatokban című részben.

Ha két sorozat konvergens, akkor a megengedett műveletek elvégzése után kapott sorozat is konvergens. Erről szól az alábbi tétel, melyet most nem bizonyítunk. Ha valakit érdekelnek a további részletek, akkor neki ajánljuk a yotub csatornánkon található Határérték és műveletek című videónkat. Ez ITT található.

Tétel: Ha az (a_n) és a (b_n) sorozatok konvergensek és az (a_n) sorozat határértéke A, a (b_n) sorozaté pedig B, akkor

• (a_n+b_n), illetve (a_n–b_n) sorozat is konvergens és határértéke A+B, illetve A-B;
• (a_nb_n) sorozat is konvergens és határértéke AB;
• (a_n/b_n) sorozat is konvergens és határértéke A/B, ahol a (b_n) sorozat tagjai és B is nullától különböző valós számok.

***

Határérték és egyenlőtlenségek

Az egyenlőtlenségek jól használhatók sorozatok konvergenciájának igazolásához. Ezek közül különösen fontos az úgynevezett rendőr-elv. A tétel onnan kapta a nevét, hogy ha két rendőr közrefog egy gyanúsítottat és a a két rendőr az őrszobához tart, akkor a gyanúsított is kénytelen oda menni.

Most csak kimondjuk a tételt. Nem bizonyítjuk. A tétel bizonyítása, valamint további egyenlőtlenségek találhatók a Határérték és egyenlőtlenségek című videónkban, ami ITT érhető el.

A rendőr-elv

Tétel: Ha

a_n \leq b_n\leq c_n

minden pozitív egész n esetén és

\lim_{n\rightarrow \infty}a_n=\lim_{n\rightarrow \infty}c_n=A, 

akkor

\lim_{n\rightarrow \infty}b_n=A.

***

Végtelenhez (mínusz végtelenhez) tartó sorozatok

Azt már korábban írtuk, hogy azokat a sorozatokat, melyek nem konvergensek, divergens sorozatoknak nevezzük. Ezek közül külön kiemeljük azokat, melyek minden határon túl nőnek, vagy csökkennek.

Mit is jelent ez? Hogy lehet ezt pontosan megfogalmazni? Nézzünk erre egy példát!

3. példa: Tekintsük az

a_n=a^n\text{ }\text{ (a>1)}

sorozatot. Bizonyítsuk be, hogy is adunk meg K valós számot, valamely tagtól kezdve a sorozat összes tagja nagyobb ennél a K számnál!

Megoldás:

Bármely nem pozitív számnál nagyobb a sorozat minden tagja.

Így legyen a K tetszőlegesen rögzített pozitív valós szám.

A megoldáshoz felhasználjuk a binomiális tételt, miszerint

(a+b)^n=\begin{pmatrix} n \\ 0 \end{pmatrix}a^n+\begin{pmatrix} n \\ 1 \end{pmatrix}a^{n-1}b+...+\begin{pmatrix} n \\ k \end{pmatrix}a^{n-k}b^k+...+\begin{pmatrix} n \\ n \end{pmatrix}b^n.

Mivel a>1, így a-1>0. Most alkalmazzuk a binomiális tételt az alábbi módon:

a^n=(1+(a-1))^n=\begin{pmatrix} n \\ 0 \end{pmatrix}1^n+\begin{pmatrix} n \\ 1 \end{pmatrix}1^{n-1}(a-1)+...+\begin{pmatrix} n \\ k \end{pmatrix}1^{n-k}(a-1)^k+...+\begin{pmatrix} n \\ n \end{pmatrix}(a-1)^n.

Mivel a-1>0, így csökkentjük a kifejezés értékét, ha az összegnek csak az első két tagját tartjuk meg és ez alapján adjuk meg a N küszöbszámot.

Így

a^n>\begin{pmatrix} n \\ 0 \end{pmatrix}1^n+\begin{pmatrix} n \\ 1 \end{pmatrix}1^{n-1}(a-1)=1+n(a-1)>K.

Ezen utolsó egyenlőtlenség pontosan akkor teljesül, ha

n>\frac{K-1}{a-1}=N.

A N számot itt is küszöbszámnak nevezzük.

Tehát, ha

n>\frac{K-1}{a-1}=N,

akkor

a^n>K.

Ezzel a feladatot megoldottuk.

***

Ha egy sorozatra teljesül az, amit az előző példában beláttunk, akkor azt mondjuk, hogy a sorozat tart a végtelenbe.

Fogalmazzuk meg az ehhez tartozó definíciót.

Definíció: Azt mondjuk, hogy az (a_n ) sorozat tart a végtelenbe, vagy határértéke végtelen, ha minden K valós számhoz létezik olyan N küszöbszám, hogy ha n>N, akkor a_n >K.

Jelölés:

\lim_{n\rightarrow\infty}a_n=\infty

Annak megfogalmazását, hogy mikor mondjuk egy sorozatról, hogy a határértéke mínusz végtelen, a tisztelt Olvasóra bízzuk.

Annak, hogy milyen egyenlőtlenségeket, illetve műveleti tételeket fogalmazhatunk meg a végtelenhez (mínusz végtelenhez) tartó sorozatokkal kapcsolatban a youtube csatornánkon található videókban lehet utána nézni. Ezeke a már korábban is említett Határérték és egyenlőtlenségek, illetve Határérték és műveletek című videók.

***

Nevezetes sorozatok határértéke

Létezik néhány olyan sorozat, melyek konvergenciájáról érdemes tudni, határértékét érdemes ismerni. Ezekt ebben a cikkben csak fesoroljuk. A velük kapcsolatos részletesebb ismereteket a youtube csatornánkon megtaláljátok. A videókat alábbiakban belinkeljük.

• 1. sorozat:

a_n=n^p \text{, }\text{ } p\in\mathbb{Z}

Konvergenciaviszonyok:

\lim_{n\rightarrow\infty}n^p=\begin{cases} \infty \text{, ha}\text{  } p>0,\\ 1, \text{ ha}\text{  } p=0,\\ 0, \text{ ha}\text{  }p<0. \end{cases}  

További részletek ITT.

• 2. sorozat:

a_n=q^n\text{, }\text{ ahol } q\neq0

Konvergenciaviszonyok:

\lim_{n\rightarrow\infty}q^n=\begin{cases} \infty \text{, ha}\text{  } q>1,\\ 1, \text{ ha}\text{  } q=1,\\ 0, \text{ ha}\text{  }|q|<1. \end{cases}  

Ha q nem nagyobb -1-nél, akkor a sorozat divergens.

További részletek ITT.

• 3. sorozat(ok):

a_n=\sqrt[n]{a}\text{ (a>0)}, \text{ }b_n=\sqrt[n]{n}

Konvergenciaviszonyok:

\lim_{n\rightarrow\infty}\sqrt[n]{a}=1\text{, } \text{ }\text{ }\lim_{n\rightarrow\infty}\sqrt[n]{n}=1

További részletek ITT.

• 4. sorozat:

a_n=\left(1+\frac{1}{n}\right)^n

Konvergenciaviszonyok:

\lim_{n\rightarrow\infty}\left(1+\frac{1}{n}\right)^n=e.

További részletek ITT.

***

Sorozatok határértéke feladatokban

Bevezető feladatok

• 1. feladat: Létezik-e határértéke az alábbi sorozatoknak? Ha igen, akkor adjuk meg!

\text{a) }a_n=\frac{-2n+7}{7n+5}; \text{ }\text{ }\text{b) } b_n=\frac{3n^2+2n-5}{n^3-n+1};

\text{c) }c_n=\frac{-2n^2+6n+7}{5n-2}; \text{ }\text{ }\text{d)} \text{ } d_n=\frac{5^{n+1}-3^n+7}{2\cdot5^n+3\cdot4^n}

Megoldás:

a)

A konvergenciaviszonyok vizsgálatához alakítsukát a törtet, majd alkalmazzuk a konvergens sorozatokra vonatkozó műveleti tételeket!

Emwljük ki a számlálóból, illetve a nevezőből a bennük szereplő legmagasabb fokú tagot, itt n-et, majd alkalmazzuk a műveleti tételeket

\lim_{n\rightarrow\infty}a_n=\lim_{n\rightarrow\infty}\frac{-2n+7}{7n+5}=\lim_{n\rightarrow\infty}\frac{n}{n}\cdot\frac{-2+\frac{7}{n}}{7+\frac{5}{n}}=-\frac{2}{7}.

Itt felhasználtuk azt is, hogy

\lim_{n\rightarrow\infty}\frac{1}{n}=0, 

így

\lim_{n\rightarrow\infty}\frac{7}{n}=0 \text{ és} \text{ }\lim_{n\rightarrow\infty}\frac{5}{n}=0.

b)

Az a) részben látott módon alakítsuk át a törtet. Azaz emeljük ki a számlálóból az n² -ont, a nevezőből az az n³ -ont, majd alkalmazzuk a műveleti tételeket

\lim_{n\rightarrow\infty}b_n=\lim_{n\rightarrow\infty}\frac{3n^2+2n-5}{n^3-n+1}=\lim_{n\rightarrow\infty}\frac{n^2}{n^3}\cdot\frac{3+\frac{2}{n}-\frac{5}{n^2}}{1-\frac{1}{n^2}-\frac{1}{n^3}}=\lim_{n\rightarrow\infty}\frac{1}{n}\cdot\frac{3+\frac{2}{n}-\frac{5}{n^2}}{1-\frac{1}{n^2}-\frac{1}{n^3}}=0.

Itt felhasználtuk azt is, hogy

\lim_{n\rightarrow\infty}\frac{1}{n}=\lim_{n\rightarrow\infty}\frac{1}{n^2}=\lim_{n\rightarrow\infty}\frac{1}{n^3}=0.

c)

Járjunk el az előzőekhez hasonló módon:

\lim_{n\rightarrow\infty}c_n=\lim_{n\rightarrow\infty}\frac{-2n^2+6n+7}{5n-2}=\lim_{n\rightarrow\infty}\frac{n^2}{n}\cdot\frac{-2+\frac{6}{n}+\frac{7}{n^2}}{5-\frac{2}{n}}=\lim_{n\rightarrow\infty}n\cdot\frac{-2+\frac{6}{n}+\frac{7}{n^2}}{5-\frac{2}{n}}=-\infty.

d)

Ugyan azt a módszert használjuk, mint eddig csak most a legnagyobb alapú exponenciális tagot emeljük ki a számlálóból, illetve a nevezőből. Ezután alkalmazzuk a q_ⁿ (|q|<1)sorozat határértékére vonatkozó ismereteket, illetve a műveleti tételeket:

\lim_{n\rightarrow\infty}d_n=\lim_{n\rightarrow\infty}\frac{5^{n+1}-3^n+7}{2\cdot5^n+3\cdot4^n}=\lim_{n\rightarrow\infty}\frac{5-\left(\frac{3}{5}\right)^n+7\cdot\left(\frac{1}{5}\right)^n}{2+3\cdot\left(\frac{4}{5}\right)^n}=\frac{5}{2}.

***

Sorozatok határértéke emelt szintű érettségi feladatban

• 2. feladat (2015. május emelt matek érettségi 7. feladat) Egy pénzintézet a tőle felvett H forint összegű hitel visszafizetésekor havi p%-os kamattal számol (p > 0), ezért az adós havi törlesztőrészletét a

t_n=H\cdot\frac{q^n(q-1)}{q^n-1}

• képlettel számítja ki (minden hónapban ekkora összeget kell visszafizetni). A képletben

q=1+\frac{p}{100},

• az n pedig azt jelenti, hogy összesen hány hónapig fizetjük a törlesztőrészleteket (ez a hitel futamideje).

• a) Fogyasztási cikkek vásárlására 1,6 millió forint hitelt vettünk fel a pénzintézettől; a havi kamat 2%. Összesen hány forintot fizetünk vissza, ha 72 hónap alatt törlesztjük a felvett hitelt? Válaszát ezer forintra kerekítve adja meg!
• b) Legkevesebb hány hónapos futamidőre vehetünk fel egy 2 millió forintos hitelt, ha legfeljebb 60 ezer forintot tudunk havonta törleszteni, és a havi kamat 2%-os?
• c) Számítsa ki a t_n sorozat határértéket, ha q = 1,02 és H = 2 000 000.

Megoldás:

a) Mivel a a hitel 1,6 millió, így H=1600000, a kamat 2%, így q=1,02, a futamidő 72 hónap, így n=72.

Így a havi törlesztés összege

t_{72}=1600000\cdot\frac{1,02^{72}(1,02-1)}{1,02^{72}-1}\approx42123.

Ezt 72 hónapra számolva kapjuk, hogy

72\cdot t_{72}=72\cdot 42123=3032856\approx3033000\text{ Ft}.

b)

Ebben a részben H=2000000, q=1,02 és a fizetendő törlesztőrészlet maximum 60000 Ft. Keresett érték az n, azaz a futamidő.

A feladatban felírt képletet felhasználva az alábbi egyenlőtlenséget írhatjuk fel:

t_{n}=2000000\cdot\frac{1,02^{n}(1,02-1)}{1,02^{n}-1}\leq60000.

Ebből fejezzük ki az 1,02ⁿ -t az alábbi módon:

\frac{1,02^{n}(1,02-1)}{1,02^{n}-1}\leq0,03,

1,02^n\cdot0,02\leq0,03(1,02^n-1),

0,03\leq0,01\cdot1,02^n,

3\leq1,02^n.

Ebből már könnynen kifejezhetjük az n-t, ha vesszük mindkét oldal tízes alapú logaritmusát, majd rendezzük az egyenlőtelnséget, felhasználva a hatvány logaritmusára vonatkozó azonosságot. Közben kihasználjuk, hogy a tízes alapú logaritmus függvény szigorúan monoton növekvő.

Így kapjuk, hogy

\lg3\leq n\cdot\lg1,02, 

\frac{\lg3}{\lg1,02}\leq n,

azaz

55,48\leq n.

Tehát legalább 56 hónapos futamidőra van szükség.

***

c)

Ebben a részben a t_n sorozat határértékét kell meghatároznunk H=2000000 és q=1,02 értékek mellett.

\lim_{n\rightarrow\infty}2000000\cdot\frac{1,02^{n}\cdot0,02}{1,02^{n}-1}=\lim_{n\rightarrow\infty}40000\cdot\frac{1,02^{n}}{1,02^{n}-1}=\lim_{n\rightarrow\infty}40000\cdot\frac{1}{1-\left(\frac{1}{1,02}\right)^n}=40000.

Tehát a határérték 40000.

***

Összefoglalás

A Sorozatok határértéke című cikkben bevezető példák után megismerkedtünk a konvergens sorozat fogalmával. Ezután foglalkoztunk a konvergens sorozatok két tulajdonságával, a műveleti tételeikkel a rendőr-elvvel és a végtelenbe tartó sorpzatokkal. Felvázoltuk néhány fontos sorozat konvergencia viszonyait is. Végül feladatok megoldásával mélyítettük el az ismereteket.

Szeretnél még több, hasonló cikket olvasni? Akkor böngéssz a blogunkon Matekos blog! Emelt szintű érettségire készülsz, vagy elsőéves egyetemista vagy? Ekkor ajánljuk figyelmedbe az online tanuló felületünket és a felkészülést segítő csomagjainkat. Az ezekkel kapcsolatos részletekről itt ÉrettségiPro+ olvashatsz.

Összegyűjtöttük az eddigi összes emelt szintű matematika érettségi feladatsort és a megoldásokat. Ezt a gyűjteményt, valamint az érettségire készüléssel kapcsolatos hasznos tanácsokat a Emelt szintű matematika feladatsorok linken érheted el.

Szerző: Ábrahám Gábor (szakmai önéletrajz)

Cikkek

A szerző további cikkei megtalálhatók a Budapesti Fazekas Milyály Gyakorló Általános Iskola és Gimnázium matematika oktatási portálján:

• Feladatok megoldása az analízis eszközeivel.
• Függvény és inverze egyenletekben
• A háromszög területe
• Polinomalgebrai feladatok
• Szélsőértékfeladatok megoldása elemi úton

Az emelt szintű érettségire készüléssel kapcsolatos írásaink a Blog linken érhetők el.

A szerző által írt tankönyvek a Maxim Kiadó linken találhatók.

Matek versenyre készülőknek

Ha olyan ambícióid vannak, hogy szeretnél matematikával versenyzés szintjén foglalkozni, akkor javaslom az Erdős Pál Matematikai Tehetségondozó Iskolát. Ezzel vonatkozó részletek ezen linken Erdős Pál Matematikai Tehetséggondozó Iskola olvashatók. A matematika versenyek témáit feldolgozó könyvek, kiadványok (a szerző Egyenlőtlenségek I.-II. című könyvei is) a MATE alapítvány, kiadványok linken kersztül vásárolhatók meg.