Az általános és középiskolai tanulmányaink során lépten nyomon találkozunk olyan feladatokkal, melyek középpontjában a trapéz szerepel. Ilyen jellegű problémák a közép-, illetve az emelt szintű érettségin is sokszor előfordulnak.
Ezért is lényeges, hogy ismerjük a legfontosabb tulajdonságait, a területének és kerületének kiszámítási módját. Az alábbi cikkben ezen ismeretek mellett olyan feladatokkal is találkozhatsz, amelyek segítik azok elmélyítését.
A feladatsor összeállításánál a fokozatosság elvét tartottam szem előtt, így azok a legegyszerűbbtől indulnak, és lépésről lépésre jutunk el az emelt szintű feladatokig.
Ezt az elvet követtem az ÉrettségiPro+ emelt szintű érettségire felkészítő tananyagának összeállításánál is.
***
Kinek hasznos az alábbi cikkünk?
Neked, ha általános iskolás vagy, és most ismerkedsz a négyszögfajtákkal.
Neked, ha érettségire készülsz, és nagyobb gyakorlatra szeretnél szert tenni geometriából.
Neked, ha esetleg már régebben voltál iskolás, ugyanakkor valamiért most szükséged lenne a trapézokkal kapcsolatos ismeretekre, és szeretnéd feleleveníteni azokat. Mi segítünk! Olvasd el cikkünket, és megtalálod a választ kérdéseidre.
***
A definíció
A trapéz olyan négyszög, melynek két oldala párhuzamos.
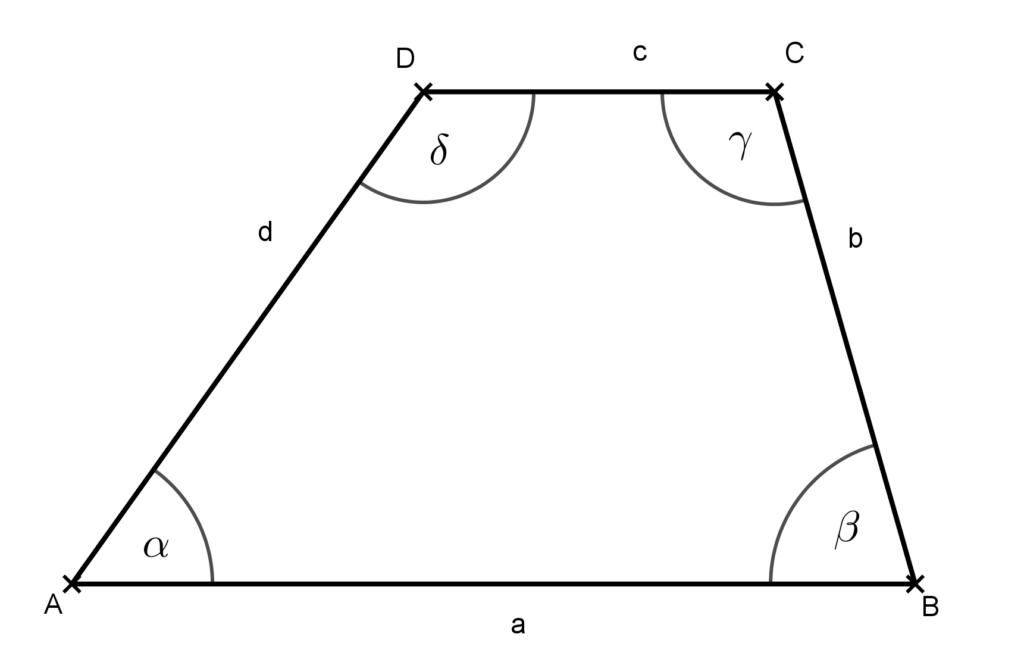
Az ábrán látható trapéz párhuzamos oldalai az AB=a és a CD=c. Ezt a két oldalt nevezzük a trapéz két alapjának. A BC=b és CD=d oldalak pedig a szárai.
A paralelogramma speciális trapéz, hisz két-két szemközti oldala párhuzamos, így van párhuzamos oldalpárja.
***
Speciális trapézok
Egyenlő szárú, szimmetrikus és húrtrapéz
Az egyenlő szárú trapéz olyan trapéz, melynek a két szára egyenlő hosszú. A paralelogramma is ilyen négyszög, hisz annak a szemközti oldalai egyenlőek.
Az olyan egyenlő szárú trapézt, melynek van köré írt köre, húrtrapéznak nevezzük. Ilyen az az egyenlő szárú trapéz, amely nem paralelogramma, illetve a téglalap. Tehát minden húrtrapéz egyenlő szárú, de nem minden egyenlő szárú trapéz húrtrapéz.
Az olyan egyenlő szárú trapézt, melynek van szimmetriatengelye, szimmetrikus trapéznak nevezzük. Ilyen az az egyenlő szárú trapéz, amely nem paralelogramma, illetve a téglalap. Tehát minden szimmetrikus trapéz egyenlő szárú, de nem minden egyenlő szárú trapéz szimmetrikus trapéz.
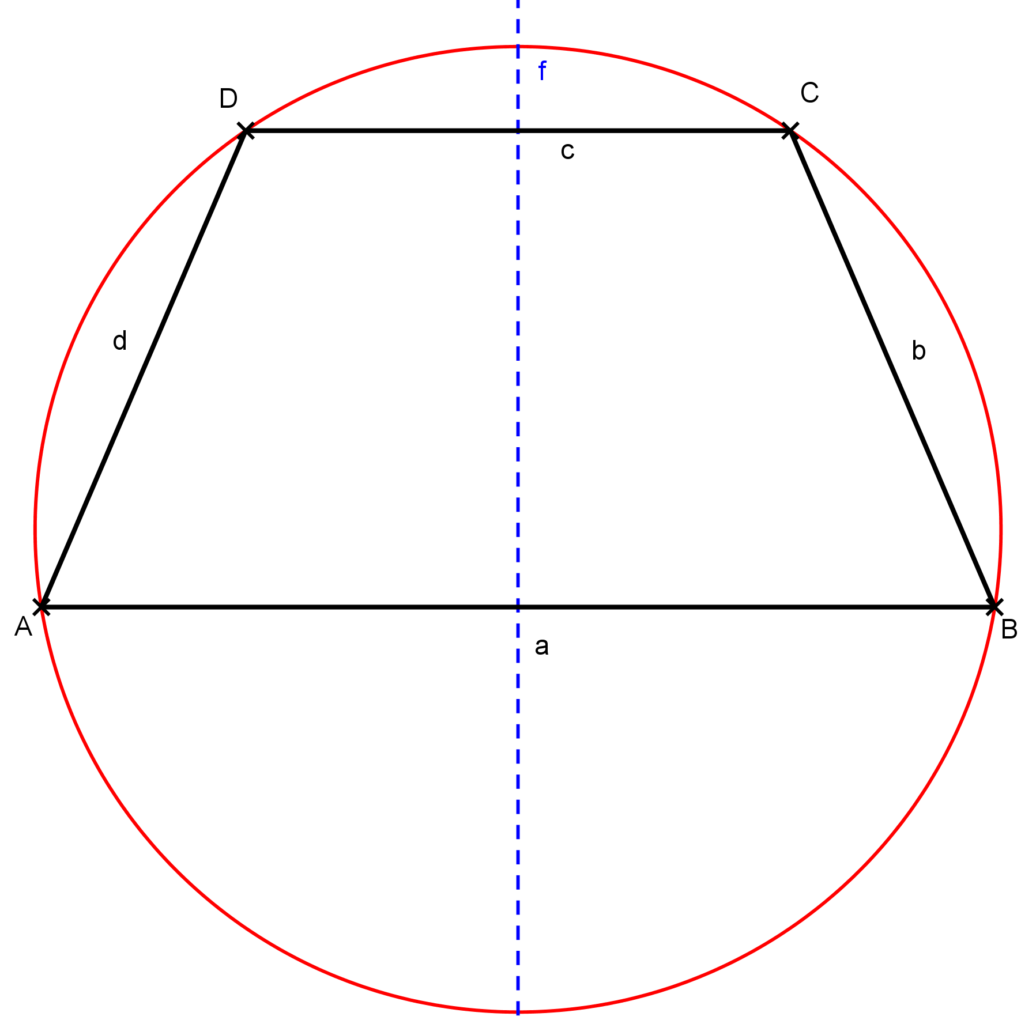
***
Derékszögű trapéz
Az olyan trapézt, melynek az egyik belső szöge 90°-os, derékszögű trapéznak nevezzük. A téglalap speciális derékszögű trapéz.
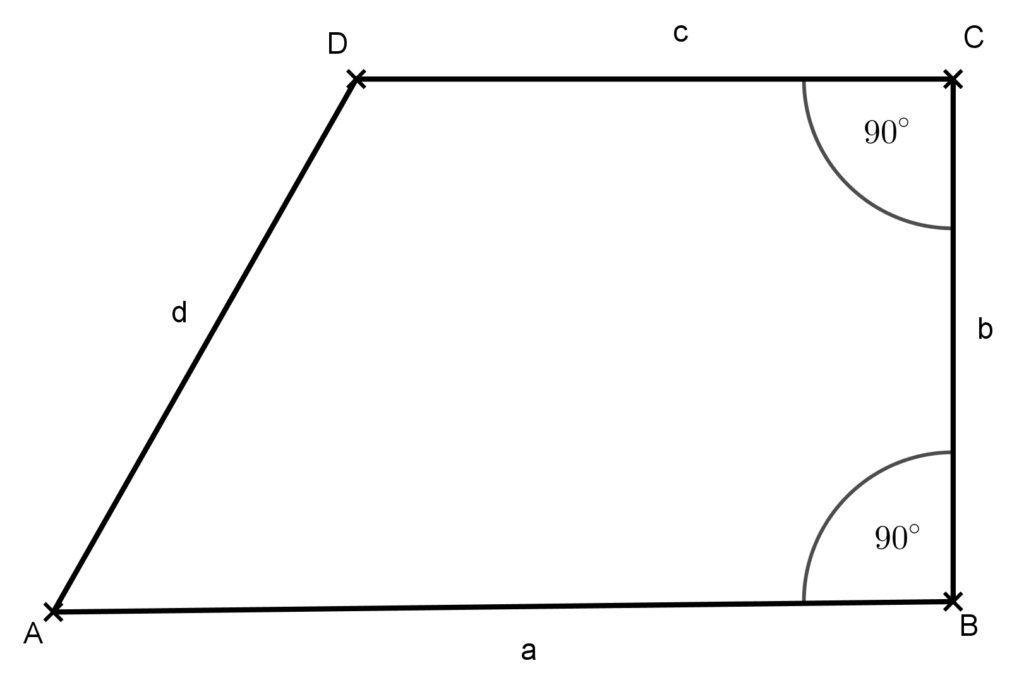
***
A tulajdonságai
A szögei
Tétel: Bármely trapézban az egy száron fekvő két szög összege 180°.
Bizonyítás: Legyenek a trapézunk csúcsai A, B, C, D, a szögei rendre α, β, γ, δ. Két alapja AB és CD. Készítsünk ábrát! Vegyük fel a B csúcsnál lévő külső szöget is!
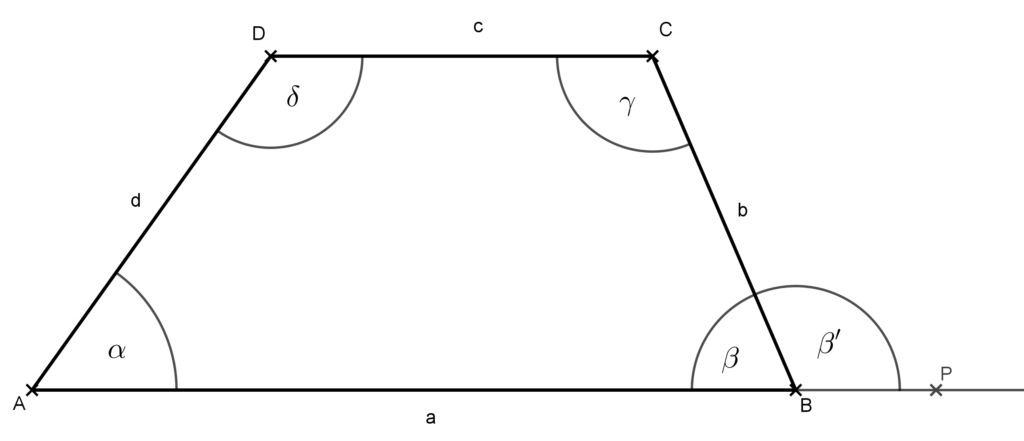
Mivel AB alapja párhuzamos a CD alappal, ezért az AB egyenese párhuzamos CD-vel. Emiatt a
\beta '=CBP\sphericalangle
váltó szöge a
\gamma =DCB\sphericalangle-\text{nek}.Tehát a két szög egyenlő. Így β=180°-β‘=180°-γ. Hasonlóan bizonyítható, hogy α+δ=180°.
Ezzel a bizonyítást befejeztük.
***
Az átlói
Tétel: Bármely trapézban az átlók az alapok arányában osztják egymást (trapéz-tétel)
Bizonyítás: Készítsünk ábrát, vegyük fel két átlóját is!
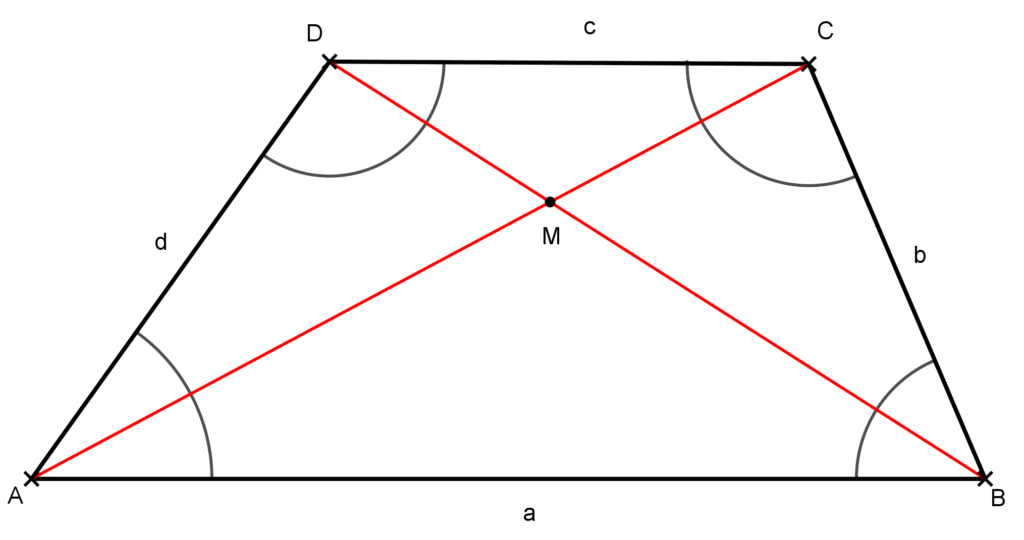
Tekintsük az ábrán az átlók által létrehozott ABM és CDM háromszögeket. Mivel a két háromszögben az ABM szög és a CDM szög, valamint az MAB szög és az MCD szög váltószögek, ezért
ABM\sphericalangle=MDC\sphericalangle \text{, valamint } MAB\sphericalangle =MCD\sphericalangle .Tehát a két háromszög két-két szöge páronként egyenlő, amiből következik, hogy hasonlók. Így megfelelő oldalaik aránya egyenlő, azaz
\frac{c}{a}=\frac{CM}{MA}=\frac{DM}{MB}.Ezt kellett bizonyítani.
***
A trapéz átlói által létrehozott háromszögek területéről
Tétel: Legyen az ABCD trapéz két alapja AB és CD, az átlóinak metszéspontja M! Az ABM és a CDM háromszögek területének aránya egyenlő az AB és CD szakaszok hossza négyzetének arányával.
Bizonyítás: Az előző tételben bizonyítottuk, hogy az ABM és a CDM háromszögek hasonlók. Ebből következik, hogy területük aránya egyenlő a megfelelő oldalaik arányának négyzetével, így
\frac{T_{ABM}}{T_{CDM}}=\left(\frac{AB}{CD}\right)^2=\frac{AB^2}{CD^2}.Ezt kellett bizonyítani.
***
Tétel: Legyen az ABCD trapéz két alapja AB és CD, szárai BC és DA, az átlóinak metszéspontja M! Az AMD és a CBM háromszögek területe egyenlő.
Bizonyítás: Készítsünk ábrát!
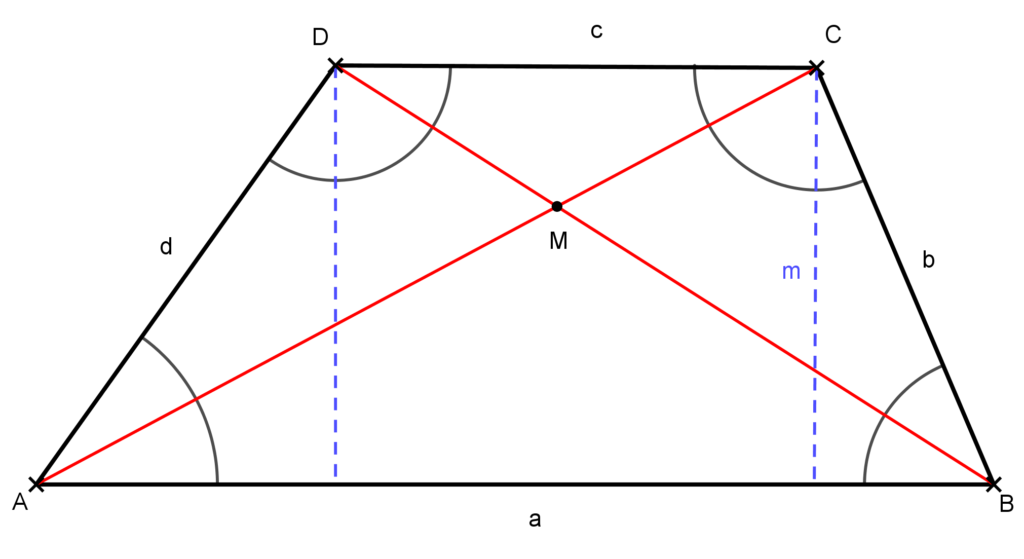
Az ábrán felvettük a C, illetve a D csúcsból a magasságot, ami a párhuzamos oldalakra merőleges egyenes trapézba eső szakasza. Legyen ez m.
Az ABC és az ABD háromszögek AB oldala közös és az ezen oldalhoz tartozó magasság mindkettőben az m. Mivel egy-egy oldaluk és a hozzá tartozó magasságuk egyenlő, így a két háromszög területe egyenlő.
Mivel
T_{ABC}=T_{ABM}+T_{MBC} \text{ és } T_{ABD}=T_{ABM}+T_{AMD},így
T_{MBC}=T_{AMD}.Amit bizonyítani akartunk.
***
A kerülete, középvonalai és területe
***
A középvonalai és területe
A középvonalai
A négyszög középvonalainak a szemközti oldalak felezőpontjait összekötő szakaszokat nevezzük. MInden négyszögnek két középvonala van.
Tehát a trapéznak is két középvonala van. Az egyik az alapok felezőpontjait, a másik pedig a szárak felezőpontjait összekötő szakasz. Általában ha trapéz középvonaláról beszélünk, akkor az utóbbit értjük alatta.
A szárakhoz tartozó középvonallal kapcsolatban fogalmazhatjuk meg az alábbi tételt.
Tétel: A trapézban a szárakhoz tartozó középvonal párhuzamos az alapjaival és hossza egyenlő az alapok hosszának számtani közepével.
Bizonyítás: A tétel bizonyítását visszavezetjük a paralelogramma középvonalára vonatkozó tételre, ami megtalálható a Paralelogramma című cikkünkben a Paralelogramma linken.
Vegyük fel az ABCD trapéz BC szárának E, illetve DA szárának F felezőpontját összekötő középvonalát! Ezután tükrözzük középpontosan a trapézt az E pontra. Készítsünk ábrát!
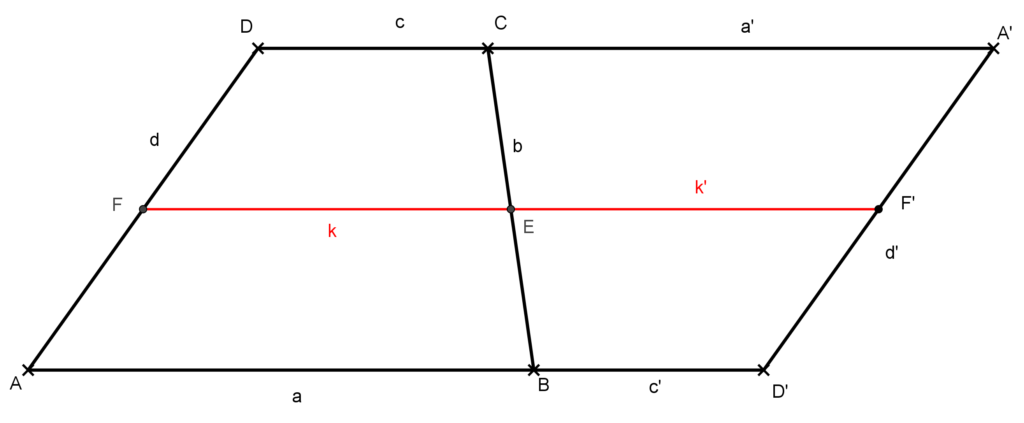
Ekkor megkapjuk az AD’A’D középpontosan szimmetrikus négyszöget, azaz paralelogrammát. A középpontos tükrözés miatt az F, E és F’ pontok egy egyenesre esnek és F’ a D’A’ oldal felezőpontja, így az FF‘ szakasz a paralelogramma középvonala, melynek az E pont felezőpontja.
Mivel a paralelogramma középvonala párhuzamos és egyenlő azzal az oldallal, mellyel nincs közös pontja, így FF’ párhuzamos és egyenlő AD’-vel.
Ebből következik, hogy FE párhuzamos AB és
FE=k=\frac{a+c}{2}.Ezt kellett bizonyítani.
***
A területe
Tétel: Ha a trapéz két alapjának a hossza a és c, valamint a magassága m, akkor területe
T=\frac{a+c}{2}\cdot{m}.Bizonyítás: Az előző tételben láttotakat figyelembe véve kapjuk, hogy az ABCD trapéz területének kétszerese egyenlő a középpontos tükrözés után keletkező AD’A’D paralelogramma területével. Mivel a paralelogramma területe egy oldalhosszának és a hozzá tartozó magassága hosszának a szorzata, így
T_{ABCD}=\frac{AD' \cdot m}{2}=\frac{a+c}{2}\cdot m.Ezt kellett bizonyítani.
***
Összefoglalás
A fenti cikkben megadtuk a trapéz területét és kerületét. Megismertük a néhány fontos tulajdonságát, foglalkoztunk a középvonalával, bebizonyítottuk a trapéz-tételt. Az ismeretek alkalmazására a Nyolc feladat trapézokra, legegyszerűbbtől emelt szintig című cikkünkben nyílik lehetőség. Ezt a cikket ITT olvashatjátok.
Szeretnél még több, hasonló cikket olvasni? Akkor böngéssz a blogunkon Matekos blog!
Ha emelt szintű érettségire készülsz, vagy elsőéves egyetemista vagy? Ekkor ajánljuk figyelmedbe az online tanuló felületünket és a felkészülést segítő csomagjainkat. Az ezekkel kapcsolatos részletekről itt ÉrettségiPro+ olvashatsz.
Összegyűjtöttük az eddigi összes emelt szintű matematika érettségi feladatsort és a megoldásokat. Ezt a gyűjteményt, valamint az érettségire készüléssel kapcsolatos hasznos tanácsokat a Emelt szintű matematika feladatsorok linken érheted el.
A szerző további cikkei megtalálhatók a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium matematika portálján ezen a linken.
Szerző: Ábrahám Gábor (szakmai önéletrajz)

